Learning-Based Modeling of Human-Autonomous Vehicle Interaction for Enhancing Safety in Mixed-Vehicle Platooning Control

As autonomous vehicles (AVs) become more prevalent on public roads, they will inevitably interact with human-driven vehicles (HVs) in mixed traffic scenarios. To ensure safe interactions between AVs and HVs, it is crucial to account for the uncertain behaviors of HVs when developing control strategies for AVs. In this paper, we propose an efficient learning-based modeling approach for HVs that combines a first-principles model with a Gaussian process (GP) learning-based component. The GP model corrects the velocity prediction of the first-principles model and estimates its uncertainty. Utilizing this model, a model predictive control (MPC) strategy, referred to as GP-MPC, was designed to enhance the safe control of a mixed vehicle platoon by integrating the uncertainty assessment into the distance constraint. We compare our GP-MPC strategy with a baseline MPC that uses only the first-principles model in simulation studies. We show that our GP-MPC strategy provides more robust safe distance guarantees and enables more efficient travel behaviors (higher travel speeds) for all vehicles in the mixed platoon. Moreover, by incorporating a sparse GP technique in HV modeling and a dynamic GP prediction in MPC, we achieve an average computation time for GP-MPC at each time step that is only 5% longer than the baseline MPC, which is approximately 100 times faster than our previous work that did not use these approximations. This work demonstrates how learning-based modeling of HVs can enhance safety and efficiency in mixed traffic involving AV-HV interaction.

Gaussian Process Learning-Based Model Predictive Control for Safe Interactions of a Platoon of Autonomous and Human-Driven Vehicles

With the continued integration of autonomous vehicles (AVs) into public roads, a mixed traffic environment with large-scale human-driven vehicles (HVs) and AVs interactions is imminent. In challenging traffic scenarios, such as emergency braking, it is crucial to account for the reactive and uncertain behavior of HVs when developing control strategies for AVs. This paper studies the safe control of a platoon of AVs interacting with a human-driven vehicle in longitudinal car-following scenarios. We first propose the use of a model that combines a first-principles model (nominal model) with a Gaussian process (GP) learning-based component for predicting behaviors of the human-driven vehicle when it interacts with AVs. The modeling accuracy of the proposed method shows a $9\%$ reduction in root mean square error (RMSE) in predicting a HV's velocity compared to the nominal model. Exploiting the properties of this model, we design a model predictive control (MPC) strategy for a platoon of AVs to ensure a safe distance between each vehicle, as well as a (probabilistic) safety of the human-driven car following the platoon. Compared to a baseline MPC that uses only a nominal model for HVs, our method achieves better velocity-tracking performance for the autonomous vehicle platoon and more robust constraint satisfaction control for a platoon of mixed vehicles system. Simulation studies demonstrate a $4.2\%$ decrease in the control cost and an approximate $1m$ increase in the minimum distance between autonomous and human-driven vehicles to better guarantee safety in challenging traffic scenarios.

On the Efficient Implementation of High Accuracy Optimality of Profile Maximum Likelihood

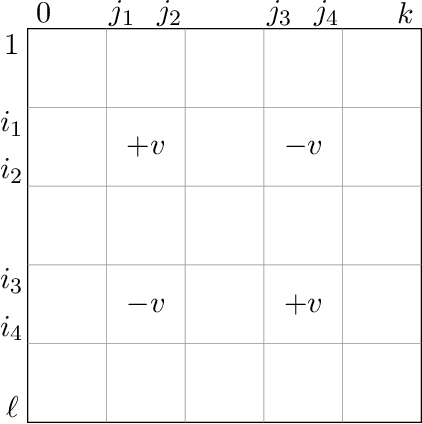
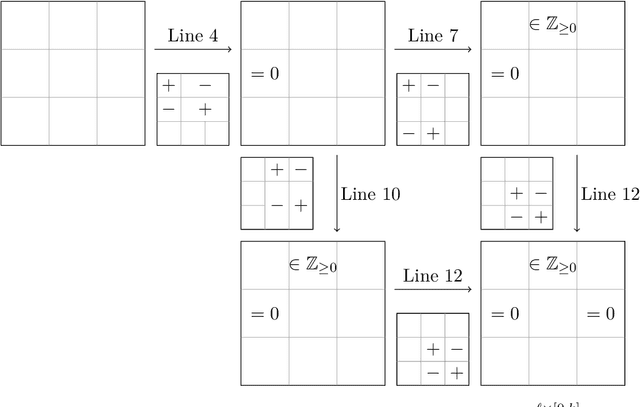
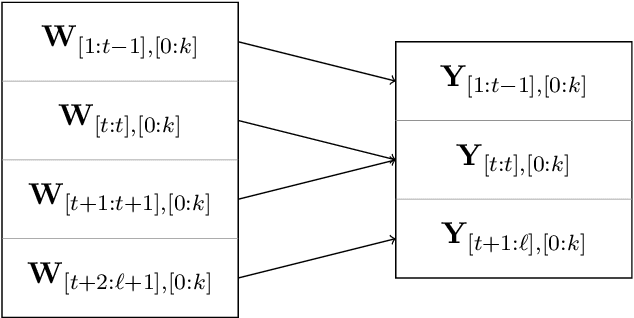
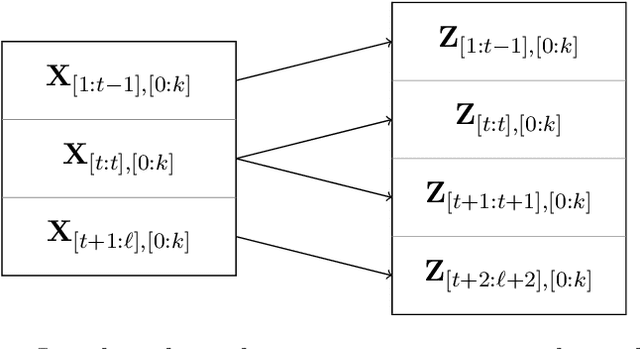
We provide an efficient unified plug-in approach for estimating symmetric properties of distributions given $n$ independent samples. Our estimator is based on profile-maximum-likelihood (PML) and is sample optimal for estimating various symmetric properties when the estimation error $\epsilon \gg n^{-1/3}$. This result improves upon the previous best accuracy threshold of $\epsilon \gg n^{-1/4}$ achievable by polynomial time computable PML-based universal estimators [ACSS21, ACSS20]. Our estimator reaches a theoretical limit for universal symmetric property estimation as [Han21] shows that a broad class of universal estimators (containing many well known approaches including ours) cannot be sample optimal for every $1$-Lipschitz property when $\epsilon \ll n^{-1/3}$.

Fair for All: Best-effort Fairness Guarantees for Classification

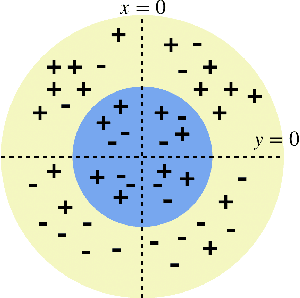
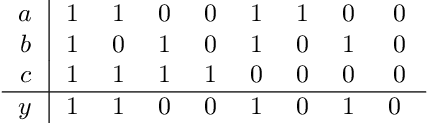
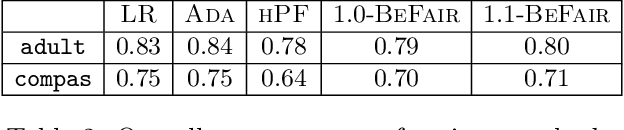
Standard approaches to group-based notions of fairness, such as \emph{parity} and \emph{equalized odds}, try to equalize absolute measures of performance across known groups (based on race, gender, etc.). Consequently, a group that is inherently harder to classify may hold back the performance on other groups; and no guarantees can be provided for unforeseen groups. Instead, we propose a fairness notion whose guarantee, on each group $g$ in a class $\mathcal{G}$, is relative to the performance of the best classifier on $g$. We apply this notion to broad classes of groups, in particular, where (a) $\mathcal{G}$ consists of all possible groups (subsets) in the data, and (b) $\mathcal{G}$ is more streamlined. For the first setting, which is akin to groups being completely unknown, we devise the {\sc PF} (Proportional Fairness) classifier, which guarantees, on any possible group $g$, an accuracy that is proportional to that of the optimal classifier for $g$, scaled by the relative size of $g$ in the data set. Due to including all possible groups, some of which could be too complex to be relevant, the worst-case theoretical guarantees here have to be proportionally weaker for smaller subsets. For the second setting, we devise the {\sc BeFair} (Best-effort Fair) framework which seeks an accuracy, on every $g \in \mathcal{G}$, which approximates that of the optimal classifier on $g$, independent of the size of $g$. Aiming for such a guarantee results in a non-convex problem, and we design novel techniques to get around this difficulty when $\mathcal{G}$ is the set of linear hypotheses. We test our algorithms on real-world data sets, and present interesting comparative insights on their performance.