On the Efficient Implementation of High Accuracy Optimality of Profile Maximum Likelihood
Paper and Code
Oct 13, 2022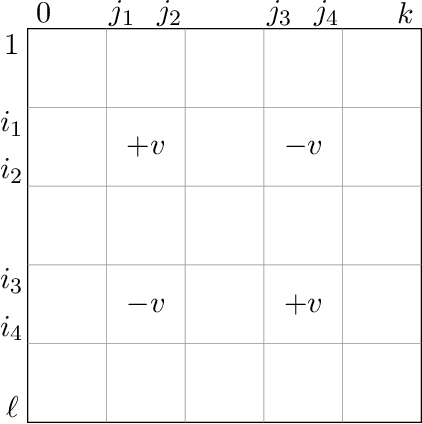
We provide an efficient unified plug-in approach for estimating symmetric properties of distributions given $n$ independent samples. Our estimator is based on profile-maximum-likelihood (PML) and is sample optimal for estimating various symmetric properties when the estimation error $\epsilon \gg n^{-1/3}$. This result improves upon the previous best accuracy threshold of $\epsilon \gg n^{-1/4}$ achievable by polynomial time computable PML-based universal estimators [ACSS21, ACSS20]. Our estimator reaches a theoretical limit for universal symmetric property estimation as [Han21] shows that a broad class of universal estimators (containing many well known approaches including ours) cannot be sample optimal for every $1$-Lipschitz property when $\epsilon \ll n^{-1/3}$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge