Shuffle and Joint Differential Privacy for Generalized Linear Contextual Bandits

We present the first algorithms for generalized linear contextual bandits under shuffle differential privacy and joint differential privacy. While prior work on private contextual bandits has been restricted to linear reward models -- which admit closed-form estimators -- generalized linear models (GLMs) pose fundamental new challenges: no closed-form estimator exists, requiring private convex optimization; privacy must be tracked across multiple evolving design matrices; and optimization error must be explicitly incorporated into regret analysis. We address these challenges under two privacy models and context settings. For stochastic contexts, we design a shuffle-DP algorithm achieving $\tilde{O}(d^{3/2}\sqrt{T}/\sqrt{\varepsilon})$ regret. For adversarial contexts, we provide a joint-DP algorithm with $\tilde{O}(d\sqrt{T}/\sqrt{\varepsilon})$ regret -- matching the non-private rate up to a $1/\sqrt{\varepsilon}$ factor. Both algorithms remove dependence on the instance-specific parameter $κ$ (which can be exponential in dimension) from the dominant $\sqrt{T}$ term. Unlike prior work on locally private GLM bandits, our methods require no spectral assumptions on the context distribution beyond $\ell_2$ boundedness.

Preference Learning with Response Time

This paper investigates the integration of response time data into human preference learning frameworks for more effective reward model elicitation. While binary preference data has become fundamental in fine-tuning foundation models, generative AI systems, and other large-scale models, the valuable temporal information inherent in user decision-making remains largely unexploited. We propose novel methodologies to incorporate response time information alongside binary choice data, leveraging the Evidence Accumulation Drift Diffusion (EZ) model, under which response time is informative of the preference strength. We develop Neyman-orthogonal loss functions that achieve oracle convergence rates for reward model learning, matching the theoretical optimal rates that would be attained if the expected response times for each query were known a priori. Our theoretical analysis demonstrates that for linear reward functions, conventional preference learning suffers from error rates that scale exponentially with reward magnitude. In contrast, our response time-augmented approach reduces this to polynomial scaling, representing a significant improvement in sample efficiency. We extend these guarantees to non-parametric reward function spaces, establishing convergence properties for more complex, realistic reward models. Our extensive experiments validate our theoretical findings in the context of preference learning over images.

Multi-Selection for Recommendation Systems

We present the construction of a multi-selection model to answer differentially private queries in the context of recommendation systems. The server sends back multiple recommendations and a ``local model'' to the user, which the user can run locally on its device to select the item that best fits its private features. We study a setup where the server uses a deep neural network (trained on the Movielens 25M dataset as the ground truth for movie recommendation. In the multi-selection paradigm, the average recommendation utility is approximately 97\% of the optimal utility (as determined by the ground truth neural network) while maintaining a local differential privacy guarantee with $\epsilon$ ranging around 1 with respect to feature vectors of neighboring users. This is in comparison to an average recommendation utility of 91\% in the non-multi-selection regime under the same constraints.

A Characterization of List Regression

There has been a recent interest in understanding and characterizing the sample complexity of list learning tasks, where the learning algorithm is allowed to make a short list of $k$ predictions, and we simply require one of the predictions to be correct. This includes recent works characterizing the PAC sample complexity of standard list classification and online list classification. Adding to this theme, in this work, we provide a complete characterization of list PAC regression. We propose two combinatorial dimensions, namely the $k$-OIG dimension and the $k$-fat-shattering dimension, and show that they optimally characterize realizable and agnostic $k$-list regression respectively. These quantities generalize known dimensions for standard regression. Our work thus extends existing list learning characterizations from classification to regression.

Query complexity of heavy hitter estimation

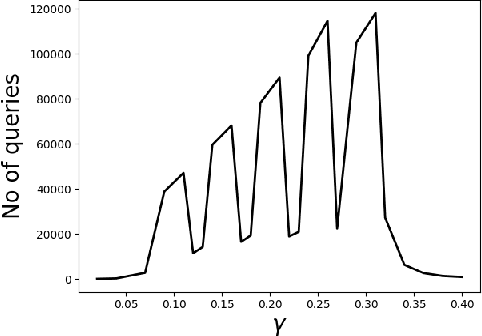
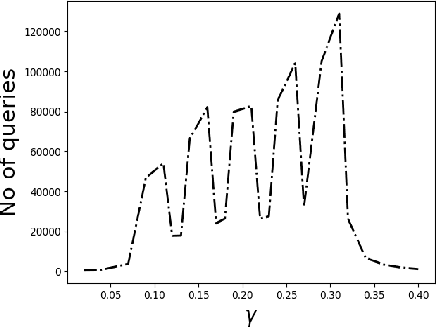
We consider the problem of identifying the subset $\mathcal{S}^{\gamma}_{\mathcal{P}}$ of elements in the support of an underlying distribution $\mathcal{P}$ whose probability value is larger than a given threshold $\gamma$, by actively querying an oracle to gain information about a sequence $X_1, X_2, \ldots$ of $i.i.d.$ samples drawn from $\mathcal{P}$. We consider two query models: $(a)$ each query is an index $i$ and the oracle return the value $X_i$ and $(b)$ each query is a pair $(i,j)$ and the oracle gives a binary answer confirming if $X_i = X_j$ or not. For each of these query models, we design sequential estimation algorithms which at each round, either decide what query to send to the oracle depending on the entire history of responses or decide to stop and output an estimate of $\mathcal{S}^{\gamma}_{\mathcal{P}}$, which is required to be correct with some pre-specified large probability. We provide upper bounds on the query complexity of the algorithms for any distribution $\mathcal{P}$ and also derive lower bounds on the optimal query complexity under the two query models. We also consider noisy versions of the two query models and propose robust estimators which can effectively counter the noise in the oracle responses.