Query complexity of heavy hitter estimation
Paper and Code
May 29, 2020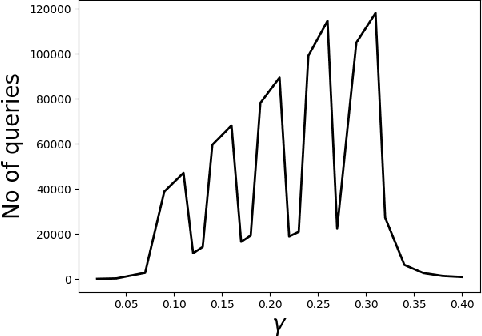
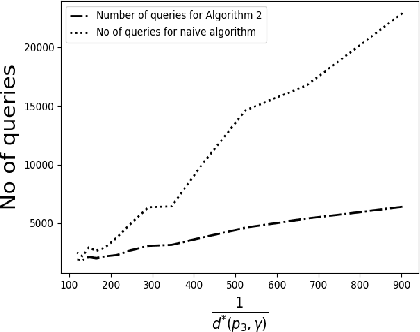
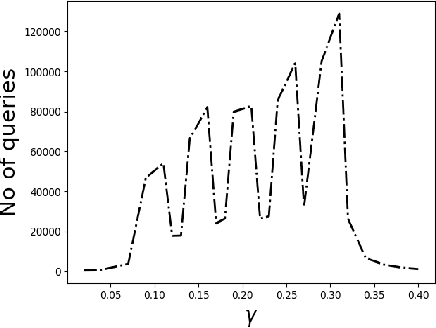
We consider the problem of identifying the subset $\mathcal{S}^{\gamma}_{\mathcal{P}}$ of elements in the support of an underlying distribution $\mathcal{P}$ whose probability value is larger than a given threshold $\gamma$, by actively querying an oracle to gain information about a sequence $X_1, X_2, \ldots$ of $i.i.d.$ samples drawn from $\mathcal{P}$. We consider two query models: $(a)$ each query is an index $i$ and the oracle return the value $X_i$ and $(b)$ each query is a pair $(i,j)$ and the oracle gives a binary answer confirming if $X_i = X_j$ or not. For each of these query models, we design sequential estimation algorithms which at each round, either decide what query to send to the oracle depending on the entire history of responses or decide to stop and output an estimate of $\mathcal{S}^{\gamma}_{\mathcal{P}}$, which is required to be correct with some pre-specified large probability. We provide upper bounds on the query complexity of the algorithms for any distribution $\mathcal{P}$ and also derive lower bounds on the optimal query complexity under the two query models. We also consider noisy versions of the two query models and propose robust estimators which can effectively counter the noise in the oracle responses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge