Fair for All: Best-effort Fairness Guarantees for Classification
Paper and Code
Jan 08, 2021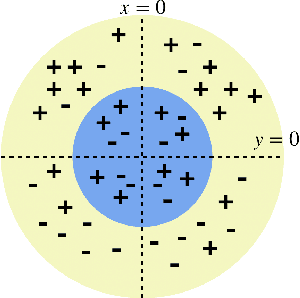
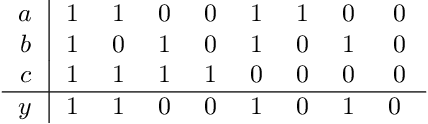
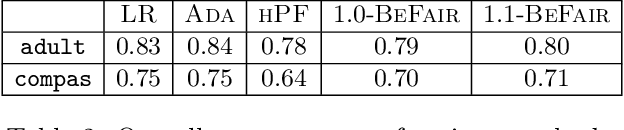

Standard approaches to group-based notions of fairness, such as \emph{parity} and \emph{equalized odds}, try to equalize absolute measures of performance across known groups (based on race, gender, etc.). Consequently, a group that is inherently harder to classify may hold back the performance on other groups; and no guarantees can be provided for unforeseen groups. Instead, we propose a fairness notion whose guarantee, on each group $g$ in a class $\mathcal{G}$, is relative to the performance of the best classifier on $g$. We apply this notion to broad classes of groups, in particular, where (a) $\mathcal{G}$ consists of all possible groups (subsets) in the data, and (b) $\mathcal{G}$ is more streamlined. For the first setting, which is akin to groups being completely unknown, we devise the {\sc PF} (Proportional Fairness) classifier, which guarantees, on any possible group $g$, an accuracy that is proportional to that of the optimal classifier for $g$, scaled by the relative size of $g$ in the data set. Due to including all possible groups, some of which could be too complex to be relevant, the worst-case theoretical guarantees here have to be proportionally weaker for smaller subsets. For the second setting, we devise the {\sc BeFair} (Best-effort Fair) framework which seeks an accuracy, on every $g \in \mathcal{G}$, which approximates that of the optimal classifier on $g$, independent of the size of $g$. Aiming for such a guarantee results in a non-convex problem, and we design novel techniques to get around this difficulty when $\mathcal{G}$ is the set of linear hypotheses. We test our algorithms on real-world data sets, and present interesting comparative insights on their performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge