Clustering without Over-Representation
Paper and Code
May 29, 2019


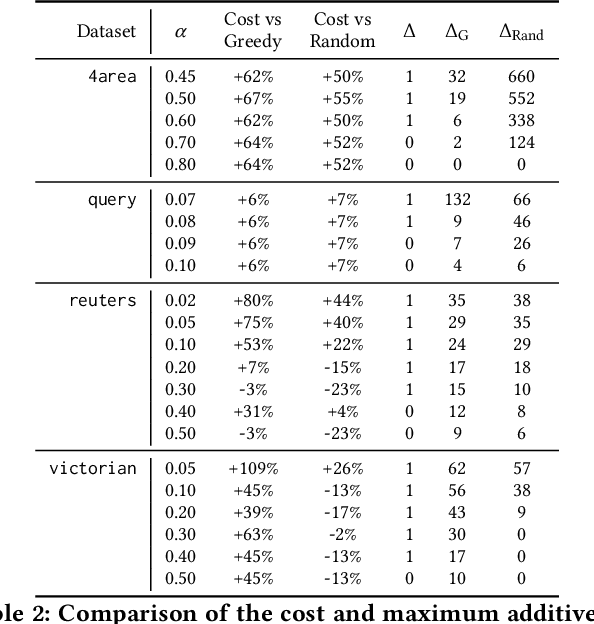
In this paper we consider clustering problems in which each point is endowed with a color. The goal is to cluster the points to minimize the classical clustering cost but with the additional constraint that no color is over-represented in any cluster. This problem is motivated by practical clustering settings, e.g., in clustering news articles where the color of an article is its source, it is preferable that no single news source dominates any cluster. For the most general version of this problem, we obtain an algorithm that has provable guarantees of performance; our algorithm is based on finding a fractional solution using a linear program and rounding the solution subsequently. For the special case of the problem where no color has an absolute majority in any cluster, we obtain a simpler combinatorial algorithm also with provable guarantees. Experiments on real-world data shows that our algorithms are effective in finding good clustering without over-representation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge