Bandits with Deterministically Evolving States
Paper and Code
Jul 21, 2023
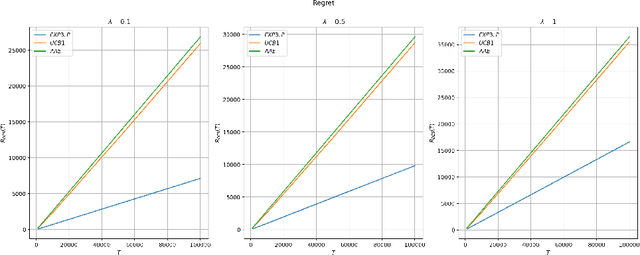
We propose a model for learning with bandit feedback while accounting for deterministically evolving and unobservable states that we call Bandits with Deterministically Evolving States. The workhorse applications of our model are learning for recommendation systems and learning for online ads. In both cases, the reward that the algorithm obtains at each round is a function of the short-term reward of the action chosen and how ``healthy'' the system is (i.e., as measured by its state). For example, in recommendation systems, the reward that the platform obtains from a user's engagement with a particular type of content depends not only on the inherent features of the specific content, but also on how the user's preferences have evolved as a result of interacting with other types of content on the platform. Our general model accounts for the different rate $\lambda \in [0,1]$ at which the state evolves (e.g., how fast a user's preferences shift as a result of previous content consumption) and encompasses standard multi-armed bandits as a special case. The goal of the algorithm is to minimize a notion of regret against the best-fixed sequence of arms pulled. We analyze online learning algorithms for any possible parametrization of the evolution rate $\lambda$. Specifically, the regret rates obtained are: for $\lambda \in [0, 1/T^2]$: $\widetilde O(\sqrt{KT})$; for $\lambda = T^{-a/b}$ with $b < a < 2b$: $\widetilde O (T^{b/a})$; for $\lambda \in (1/T, 1 - 1/\sqrt{T}): \widetilde O (K^{1/3}T^{2/3})$; and for $\lambda \in [1 - 1/\sqrt{T}, 1]: \widetilde O (K\sqrt{T})$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge