Deep Reinforcement Learning for Sequential Combinatorial Auctions

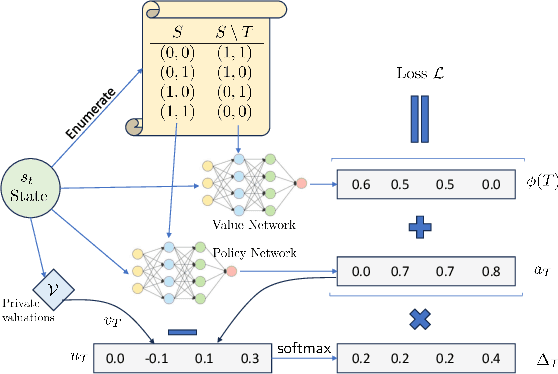
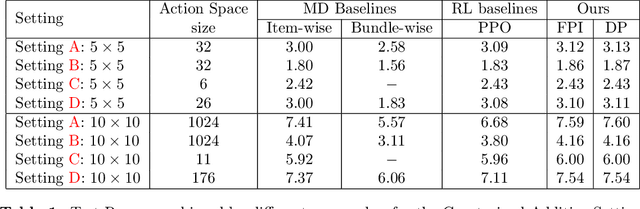
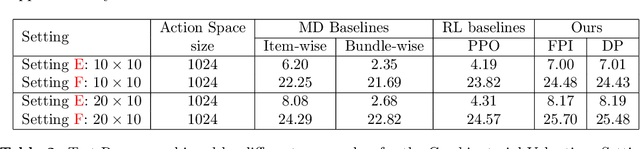
Revenue-optimal auction design is a challenging problem with significant theoretical and practical implications. Sequential auction mechanisms, known for their simplicity and strong strategyproofness guarantees, are often limited by theoretical results that are largely existential, except for certain restrictive settings. Although traditional reinforcement learning methods such as Proximal Policy Optimization (PPO) and Soft Actor-Critic (SAC) are applicable in this domain, they struggle with computational demands and convergence issues when dealing with large and continuous action spaces. In light of this and recognizing that we can model transitions differentiable for our settings, we propose using a new reinforcement learning framework tailored for sequential combinatorial auctions that leverages first-order gradients. Our extensive evaluations show that our approach achieves significant improvement in revenue over both analytical baselines and standard reinforcement learning algorithms. Furthermore, we scale our approach to scenarios involving up to 50 agents and 50 items, demonstrating its applicability in complex, real-world auction settings. As such, this work advances the computational tools available for auction design and contributes to bridging the gap between theoretical results and practical implementations in sequential auction design.

Data Market Design through Deep Learning

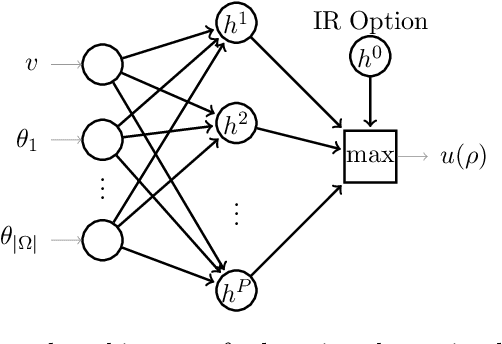
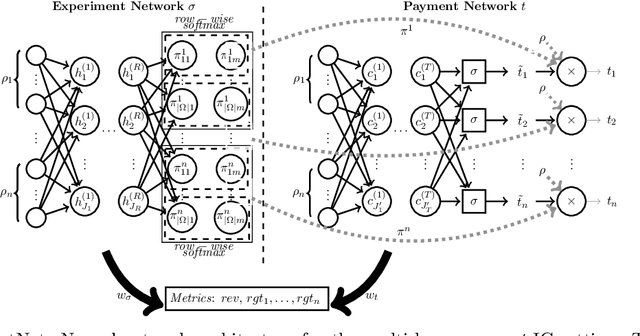
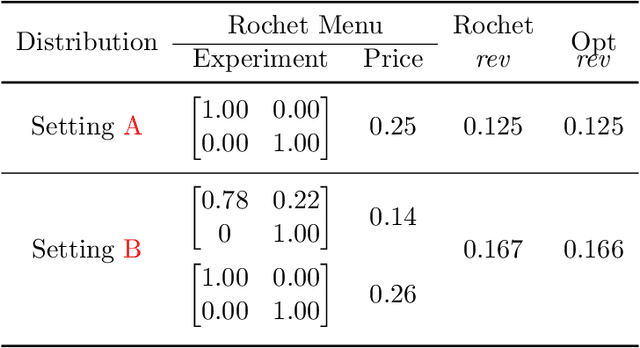
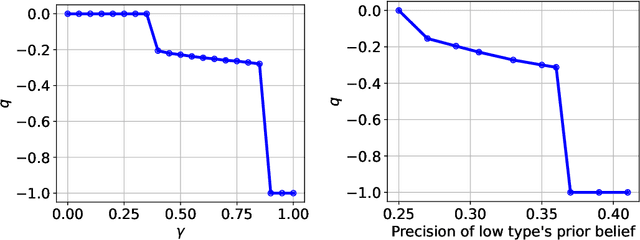
The $\textit{data market design}$ problem is a problem in economic theory to find a set of signaling schemes (statistical experiments) to maximize expected revenue to the information seller, where each experiment reveals some of the information known to a seller and has a corresponding price [Bergemann et al., 2018]. Each buyer has their own decision to make in a world environment, and their subjective expected value for the information associated with a particular experiment comes from the improvement in this decision and depends on their prior and value for different outcomes. In a setting with multiple buyers, a buyer's expected value for an experiment may also depend on the information sold to others [Bonatti et al., 2022]. We introduce the application of deep learning for the design of revenue-optimal data markets, looking to expand the frontiers of what can be understood and achieved. Relative to earlier work on deep learning for auction design [D\"utting et al., 2023], we must learn signaling schemes rather than allocation rules and handle $\textit{obedience constraints}$ $-$ these arising from modeling the downstream actions of buyers $-$ in addition to incentive constraints on bids. Our experiments demonstrate that this new deep learning framework can almost precisely replicate all known solutions from theory, expand to more complex settings, and be used to establish the optimality of new designs for data markets and make conjectures in regard to the structure of optimal designs.

Deep Learning for Two-Sided Matching

We initiate the use of a multi-layer neural network to model two-sided matching and to explore the design space between strategy-proofness and stability. It is well known that both properties cannot be achieved simultaneously but the efficient frontier in this design space is not understood. We show empirically that it is possible to achieve a good compromise between stability and strategy-proofness-substantially better than that achievable through a convex combination of deferred acceptance (stable and strategy-proof for only one side of the market) and randomized serial dictatorship (strategy-proof but not stable).

From Predictions to Decisions: Using Lookahead Regularization

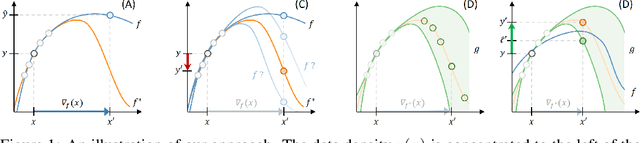
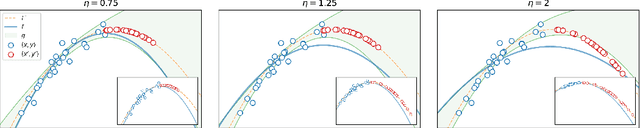
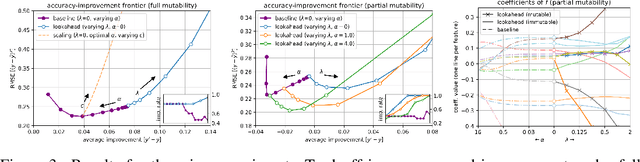
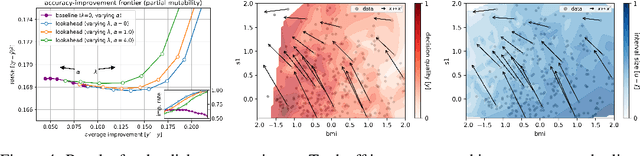
Machine learning is a powerful tool for predicting human-related outcomes, from credit scores to heart attack risks. But when deployed, learned models also affect how users act in order to improve outcomes, whether predicted or real. The standard approach to learning is agnostic to induced user actions and provides no guarantees as to the effect of actions. We provide a framework for learning predictors that are both accurate and promote good actions. For this, we introduce look-ahead regularization which, by anticipating user actions, encourages predictive models to also induce actions that improve outcomes. This regularization carefully tailors the uncertainty estimates governing confidence in this improvement to the distribution of model-induced actions. We report the results of experiments on real and synthetic data that show the effectiveness of this approach.