Deep Reinforcement Learning for Sequential Combinatorial Auctions
Paper and Code
Jul 10, 2024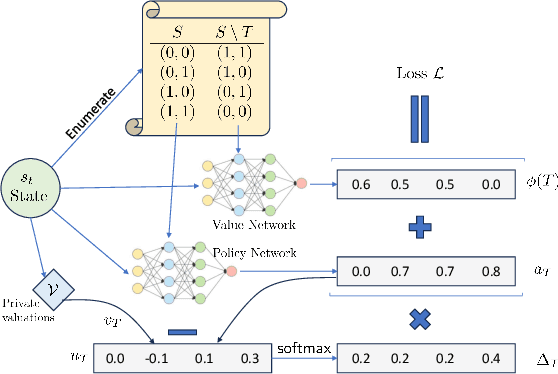
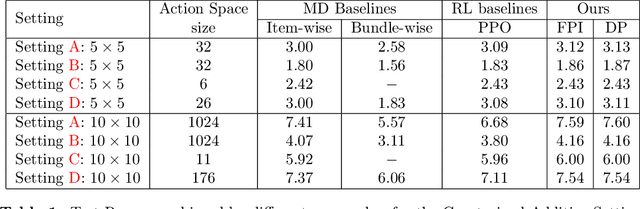
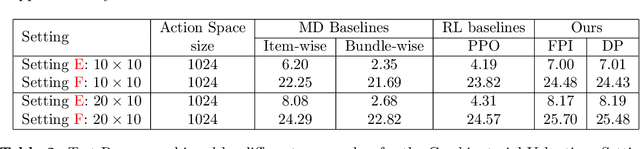

Revenue-optimal auction design is a challenging problem with significant theoretical and practical implications. Sequential auction mechanisms, known for their simplicity and strong strategyproofness guarantees, are often limited by theoretical results that are largely existential, except for certain restrictive settings. Although traditional reinforcement learning methods such as Proximal Policy Optimization (PPO) and Soft Actor-Critic (SAC) are applicable in this domain, they struggle with computational demands and convergence issues when dealing with large and continuous action spaces. In light of this and recognizing that we can model transitions differentiable for our settings, we propose using a new reinforcement learning framework tailored for sequential combinatorial auctions that leverages first-order gradients. Our extensive evaluations show that our approach achieves significant improvement in revenue over both analytical baselines and standard reinforcement learning algorithms. Furthermore, we scale our approach to scenarios involving up to 50 agents and 50 items, demonstrating its applicability in complex, real-world auction settings. As such, this work advances the computational tools available for auction design and contributes to bridging the gap between theoretical results and practical implementations in sequential auction design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge