Regression as Classification: Influence of Task Formulation on Neural Network Features
Paper and Code
Nov 10, 2022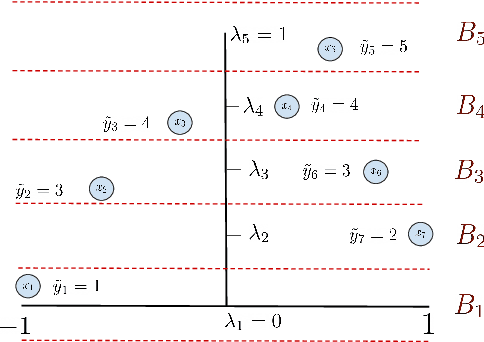
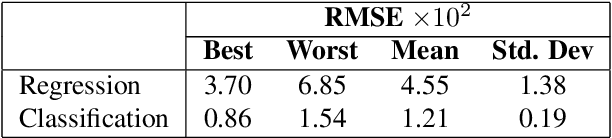
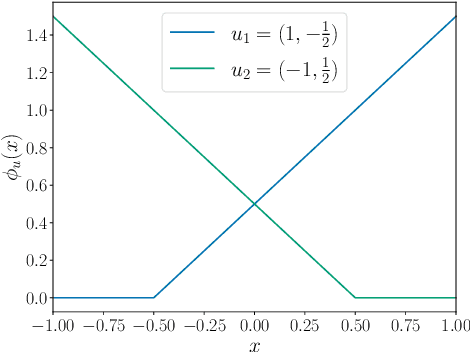
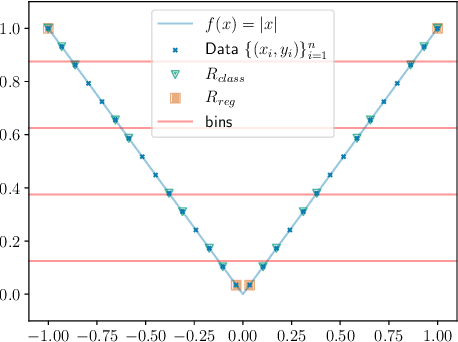
Neural networks can be trained to solve regression problems by using gradient-based methods to minimize the square loss. However, practitioners often prefer to reformulate regression as a classification problem, observing that training on the cross entropy loss results in better performance. By focusing on two-layer ReLU networks, which can be fully characterized by measures over their feature space, we explore how the implicit bias induced by gradient-based optimization could partly explain the above phenomenon. We provide theoretical evidence that the regression formulation yields a measure whose support can differ greatly from that for classification, in the case of one-dimensional data. Our proposed optimal supports correspond directly to the features learned by the input layer of the network. The different nature of these supports sheds light on possible optimization difficulties the square loss could encounter during training, and we present empirical results illustrating this phenomenon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge