Efficient and Modular Implicit Differentiation

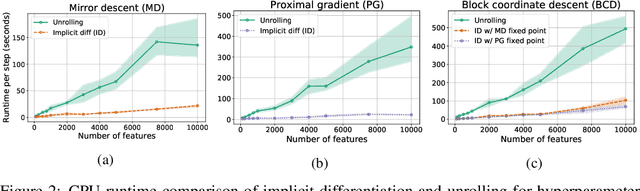
Automatic differentiation (autodiff) has revolutionized machine learning. It allows expressing complex computations by composing elementary ones in creative ways and removes the burden of computing their derivatives by hand. More recently, differentiation of optimization problem solutions has attracted widespread attention with applications such as optimization as a layer, and in bi-level problems such as hyper-parameter optimization and meta-learning. However, the formulas for these derivatives often involve case-by-case tedious mathematical derivations. In this paper, we propose a unified, efficient and modular approach for implicit differentiation of optimization problems. In our approach, the user defines (in Python in the case of our implementation) a function $F$ capturing the optimality conditions of the problem to be differentiated. Once this is done, we leverage autodiff of $F$ and implicit differentiation to automatically differentiate the optimization problem. Our approach thus combines the benefits of implicit differentiation and autodiff. It is efficient as it can be added on top of any state-of-the-art solver and modular as the optimality condition specification is decoupled from the implicit differentiation mechanism. We show that seemingly simple principles allow to recover many recently proposed implicit differentiation methods and create new ones easily. We demonstrate the ease of formulating and solving bi-level optimization problems using our framework. We also showcase an application to the sensitivity analysis of molecular dynamics.