Machine-learning physics from unphysics: Finding deconfinement temperature in lattice Yang-Mills theories from outside the scaling window

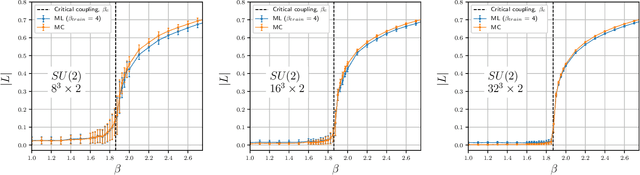
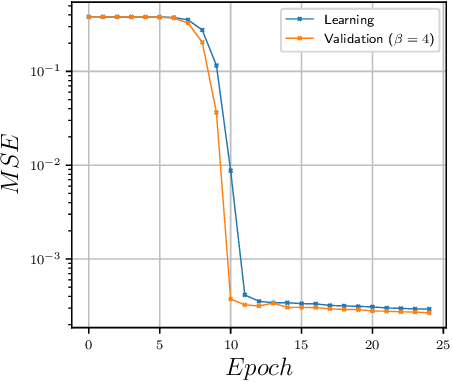
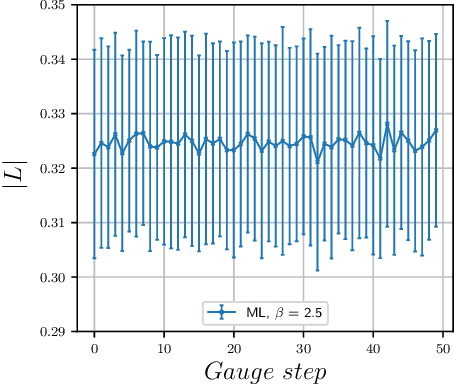
We study the machine learning techniques applied to the lattice gauge theory's critical behavior, particularly to the confinement/deconfinement phase transition in the SU(2) and SU(3) gauge theories. We find that the neural network of the machine-learning algorithm, trained on 'bare' lattice configurations at an unphysical value of the lattice parameters as an input, builds up a gauge-invariant function, and finds correlations with the target observable that is valid in the physical region of the parameter space. In particular, if the algorithm aimed to predict the Polyakov loop as the deconfining order parameter, it builds a trace of the gauge group matrices along a closed loop in the time direction. As a result, the neural network, trained at one unphysical value of the lattice coupling $\beta$ predicts the order parameter in the whole region of the $\beta$ values with good precision. We thus demonstrate that the machine learning techniques may be used as a numerical analog of the analytical continuation from easily accessible but physically uninteresting regions of the coupling space to the interesting but potentially not accessible regions.

Topological defects and confinement with machine learning: the case of monopoles in compact electrodynamics

We investigate the advantages of machine learning techniques to recognize the dynamics of topological objects in quantum field theories. We consider the compact U(1) gauge theory in three spacetime dimensions as the simplest example of a theory that exhibits confinement and mass gap phenomena generated by monopoles. We train a neural network with a generated set of monopole configurations to distinguish between confinement and deconfinement phases, from which it is possible to determine the deconfinement transition point and to predict several observables. The model uses a supervised learning approach and treats the monopole configurations as three-dimensional images (holograms). We show that the model can determine the transition temperature with accuracy, which depends on the criteria implemented in the algorithm. More importantly, we train the neural network with configurations from a single lattice size before making predictions for configurations from other lattice sizes, from which a reliable estimation of the critical temperatures are obtained.

Casimir effect with machine learning

Vacuum fluctuations of quantum fields between physical objects depend on the shapes, positions, and internal composition of the latter. For objects of arbitrary shapes, even made from idealized materials, the calculation of the associated zero-point (Casimir) energy is an analytically intractable challenge. We propose a new numerical approach to this problem based on machine-learning techniques and illustrate the effectiveness of the method in a (2+1) dimensional scalar field theory. The Casimir energy is first calculated numerically using a Monte-Carlo algorithm for a set of the Dirichlet boundaries of various shapes. Then, a neural network is trained to compute this energy given the Dirichlet domain, treating the latter as black-and-white pixelated images. We show that after the learning phase, the neural network is able to quickly predict the Casimir energy for new boundaries of general shapes with reasonable accuracy.