Deep learning complete intersection Calabi-Yau manifolds

We review advancements in deep learning techniques for complete intersection Calabi-Yau (CICY) 3- and 4-folds, with the aim of understanding better how to handle algebraic topological data with machine learning. We first discuss methodological aspects and data analysis, before describing neural networks architectures. Then, we describe the state-of-the art accuracy in predicting Hodge numbers. We include new results on extrapolating predictions from low to high Hodge numbers, and conversely.

Trustworthiness of Laser-Induced Breakdown Spectroscopy Predictions via Simulation-based Synthetic Data Augmentation and Multitask Learning

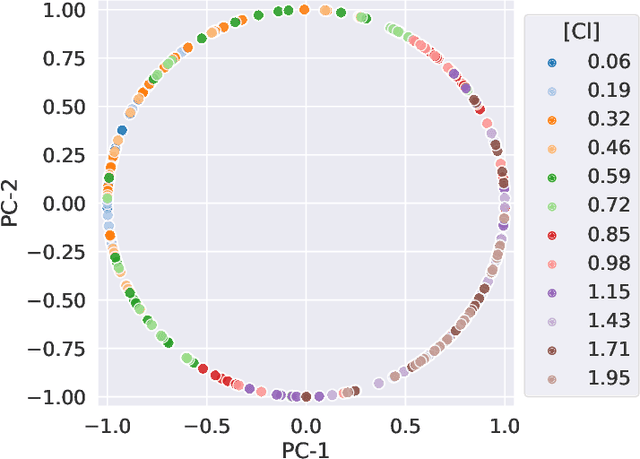
We consider quantitative analyses of spectral data using laser-induced breakdown spectroscopy. We address the small size of training data available, and the validation of the predictions during inference on unknown data. For the purpose, we build robust calibration models using deep convolutional multitask learning architectures to predict the concentration of the analyte, alongside additional spectral information as auxiliary outputs. These secondary predictions can be used to validate the trustworthiness of the model by taking advantage of the mutual dependencies of the parameters of the multitask neural networks. Due to the experimental lack of training samples, we introduce a simulation-based data augmentation process to synthesise an arbitrary number of spectra, statistically representative of the experimental data. Given the nature of the deep learning model, no dimensionality reduction or data selection processes are required. The procedure is an end-to-end pipeline including the process of synthetic data augmentation, the construction of a suitable robust, homoscedastic, deep learning model, and the validation of its predictions. In the article, we compare the performance of the multitask model with traditional univariate and multivariate analyses, to highlight the separate contributions of each element introduced in the process.

HyperPCA: a Powerful Tool to Extract Elemental Maps from Noisy Data Obtained in LIBS Mapping of Materials

Laser-induced breakdown spectroscopy is a preferred technique for fast and direct multi-elemental mapping of samples under ambient pressure, without any limitation on the targeted element. However, LIBS mapping data have two peculiarities: an intrinsically low signal-to-noise ratio due to single-shot measurements, and a high dimensionality due to the high number of spectra acquired for imaging. This is all the truer as lateral resolution gets higher: in this case, the ablation spot diameter is reduced, as well as the ablated mass and the emission signal, while the number of spectra for a given surface increases. Therefore, efficient extraction of physico-chemical information from a noisy and large dataset is a major issue. Multivariate approaches were introduced by several authors as a means to cope with such data, particularly Principal Component Analysis. Yet, PCA is known to present theoretical constraints for the consistent reconstruction of the dataset, and has therefore limitations to efficient interpretation of LIBS mapping data. In this paper, we introduce HyperPCA, a new analysis tool for hyperspectral images based on a sparse representation of the data using Discrete Wavelet Transform and kernel-based sparse PCA to reduce the impact of noise on the data and to consistently reconstruct the spectroscopic signal, with a particular emphasis on LIBS data. The method is first illustrated using simulated LIBS mapping datasets to emphasize its performances with highly noisy and/or highly interfered spectra. Comparisons to standard PCA and to traditional univariate data analyses are provided. Finally, it is used to process real data in two cases that clearly illustrate the potential of the proposed algorithm. We show that the method presents advantages both in quantity and quality of the information recovered, thus improving the physico-chemical characterisation of analysed surfaces.

Deep multi-task mining Calabi-Yau four-folds

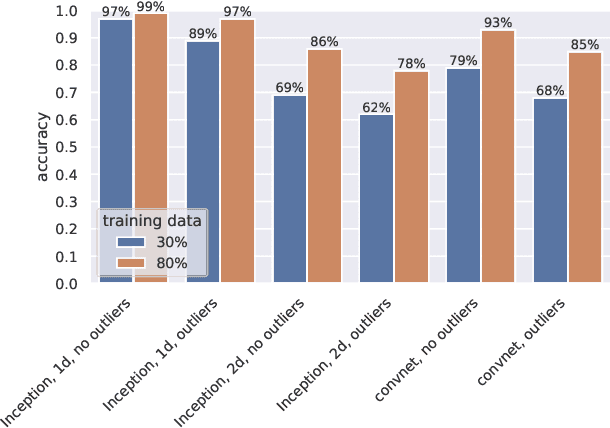
We continue earlier efforts in computing the dimensions of tangent space cohomologies of Calabi-Yau manifolds using deep learning. In this paper, we consider the dataset of all Calabi-Yau four-folds constructed as complete intersections in products of projective spaces. Employing neural networks inspired by state-of-the-art computer vision architectures, we improve earlier benchmarks and demonstrate that all four non-trivial Hodge numbers can be learned at the same time using a multi-task architecture. With 30% (80%) training ratio, we reach an accuracy of 100% for $h^{(1,1)}$ and 97% for $h^{(2,1)}$ (100% for both), 81% (96%) for $h^{(3,1)}$, and 49% (83%) for $h^{(2,2)}$. Assuming that the Euler number is known, as it is easy to compute, and taking into account the linear constraint arising from index computations, we get 100% total accuracy.

Machine learning for complete intersection Calabi-Yau manifolds: a methodological study

We revisit the question of predicting both Hodge numbers $h^{1,1}$ and $h^{2,1}$ of complete intersection Calabi-Yau (CICY) 3-folds using machine learning (ML), considering both the old and new datasets built respectively by Candelas-Dale-Lutken-Schimmrigk / Green-H\"ubsch-Lutken and by Anderson-Gao-Gray-Lee. In real world applications, implementing a ML system rarely reduces to feed the brute data to the algorithm. Instead, the typical workflow starts with an exploratory data analysis (EDA) which aims at understanding better the input data and finding an optimal representation. It is followed by the design of a validation procedure and a baseline model. Finally, several ML models are compared and combined, often involving neural networks with a topology more complicated than the sequential models typically used in physics. By following this procedure, we improve the accuracy of ML computations for Hodge numbers with respect to the existing literature. First, we obtain 97% (resp. 99%) accuracy for $h^{1,1}$ using a neural network inspired by the Inception model for the old dataset, using only 30% (resp. 70%) of the data for training. For the new one, a simple linear regression leads to almost 100% accuracy with 30% of the data for training. The computation of $h^{2,1}$ is less successful as we manage to reach only 50% accuracy for both datasets, but this is still better than the 16% obtained with a simple neural network (SVM with Gaussian kernel and feature engineering and sequential convolutional network reach at best 36%). This serves as a proof of concept that neural networks can be valuable to study the properties of geometries appearing in string theory.

Inception Neural Network for Complete Intersection Calabi-Yau 3-folds

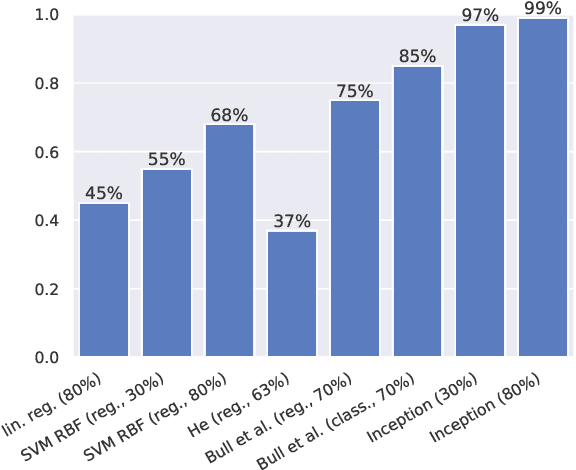
We introduce a neural network inspired by Google's Inception model to compute the Hodge number $h^{1,1}$ of complete intersection Calabi-Yau (CICY) 3-folds. This architecture improves largely the accuracy of the predictions over existing results, giving already 97% of accuracy with just 30% of the data for training. Moreover, accuracy climbs to 99% when using 80% of the data for training. This proves that neural networks are a valuable resource to study geometric aspects in both pure mathematics and string theory.