Silhouette-Guided Instance-Weighted k-means

Clustering is a fundamental unsupervised learning task with numerous applications across diverse fields. Popular algorithms such as k-means often struggle with outliers or imbalances, leading to distorted centroids and suboptimal partitions. We introduce K-Sil, a silhouette-guided refinement of the k-means algorithm that weights points based on their silhouette scores, prioritizing well-clustered instances while suppressing borderline or noisy regions. The algorithm emphasizes user-specified silhouette aggregation metrics: macro-, micro-averaged or a combination, through self-tuning weighting schemes, supported by appropriate sampling strategies and scalable approximations. These components ensure computational efficiency and adaptability to diverse dataset geometries. Theoretical guarantees establish centroid convergence, and empirical validation on synthetic and real-world datasets demonstrates statistically significant improvements in silhouette scores over k-means and two other instance-weighted k-means variants. These results establish K-Sil as a principled alternative for applications demanding high-quality, well-separated clusters.

Counterfactual Explanations for k-means and Gaussian Clustering

Counterfactuals have been recognized as an effective approach to explain classifier decisions. Nevertheless, they have not yet been considered in the context of clustering. In this work, we propose the use of counterfactuals to explain clustering solutions. First, we present a general definition for counterfactuals for model-based clustering that includes plausibility and feasibility constraints. Then we consider the counterfactual generation problem for k-means and Gaussian clustering assuming Euclidean distance. Our approach takes as input the factual, the target cluster, a binary mask indicating actionable or immutable features and a plausibility factor specifying how far from the cluster boundary the counterfactual should be placed. In the k-means clustering case, analytical mathematical formulas are presented for computing the optimal solution, while in the Gaussian clustering case (assuming full, diagonal, or spherical covariances) our method requires the numerical solution of a nonlinear equation with a single parameter only. We demonstrate the advantages of our approach through illustrative examples and quantitative experimental comparisons.

Statistical Modeling of Univariate Multimodal Data

Unimodality constitutes a key property indicating grouping behavior of the data around a single mode of its density. We propose a method that partitions univariate data into unimodal subsets through recursive splitting around valley points of the data density. For valley point detection, we introduce properties of critical points on the convex hull of the empirical cumulative density function (ecdf) plot that provide indications on the existence of density valleys. Next, we apply a unimodal data modeling approach that provides a statistical model for each obtained unimodal subset in the form of a Uniform Mixture Model (UMM). Consequently, a hierarchical statistical model of the initial dataset is obtained in the form of a mixture of UMMs, named as the Unimodal Mixture Model (UDMM). The proposed method is non-parametric, hyperparameter-free, automatically estimates the number of unimodal subsets and provides accurate statistical models as indicated by experimental results on clustering and density estimation tasks.

Optimized neural forms for solving ordinary differential equations

A critical issue in approximating solutions of ordinary differential equations using neural networks is the exact satisfaction of the boundary or initial conditions. For this purpose, neural forms have been introduced, i.e., functional expressions that depend on neural networks which, by design, satisfy the prescribed conditions exactly. Expanding upon prior progress, the present work contributes in three distinct aspects. First, it presents a novel formalism for crafting optimized neural forms. Second, it outlines a method for establishing an upper bound on the absolute deviation from the exact solution. Third, it introduces a technique for converting problems with Neumann or Robin conditions into equivalent problems with parametric Dirichlet conditions. The proposed optimized neural forms were numerically tested on a set of diverse problems, encompassing first-order and second-order ordinary differential equations, as well as first-order systems. Stiff and delay differential equations were also considered. The obtained solutions were compared against solutions obtained via Runge-Kutta methods and exact solutions wherever available. The reported results and analysis verify that in addition to the exact satisfaction of the boundary or initial conditions, optimized neural forms provide closed-form solutions of superior interpolation capability and controllable overall accuracy.

Deep Clustering Using the Soft Silhouette Score: Towards Compact and Well-Separated Clusters

Unsupervised learning has gained prominence in the big data era, offering a means to extract valuable insights from unlabeled datasets. Deep clustering has emerged as an important unsupervised category, aiming to exploit the non-linear mapping capabilities of neural networks in order to enhance clustering performance. The majority of deep clustering literature focuses on minimizing the inner-cluster variability in some embedded space while keeping the learned representation consistent with the original high-dimensional dataset. In this work, we propose soft silhoutte, a probabilistic formulation of the silhouette coefficient. Soft silhouette rewards compact and distinctly separated clustering solutions like the conventional silhouette coefficient. When optimized within a deep clustering framework, soft silhouette guides the learned representations towards forming compact and well-separated clusters. In addition, we introduce an autoencoder-based deep learning architecture that is suitable for optimizing the soft silhouette objective function. The proposed deep clustering method has been tested and compared with several well-studied deep clustering methods on various benchmark datasets, yielding very satisfactory clustering results.

Silhouette Aggregation: From Micro to Macro

Silhouette coefficient is an established internal clustering evaluation measure that produces a score per data point, assessing the quality of its clustering assignment. To assess the quality of the clustering of the whole dataset, the scores of all the points in the dataset are either (micro) averaged into a single value or averaged at the cluster level and then (macro) averaged. As we illustrate in this work, by using a synthetic example, the micro-averaging strategy is sensitive both to cluster imbalance and outliers (background noise) while macro-averaging is far more robust to both. Furthermore, the latter allows cluster-balanced sampling which yields robust computation of the silhouette score. By conducting an experimental study on eight real-world datasets, estimating the ground truth number of clusters, we show that both coefficients, micro and macro, should be considered.

UniForCE: The Unimodality Forest Method for Clustering and Estimation of the Number of Clusters

Estimating the number of clusters k while clustering the data is a challenging task. An incorrect cluster assumption indicates that the number of clusters k gets wrongly estimated. Consequently, the model fitting becomes less important. In this work, we focus on the concept of unimodality and propose a flexible cluster definition called locally unimodal cluster. A locally unimodal cluster extends for as long as unimodality is locally preserved across pairs of subclusters of the data. Then, we propose the UniForCE method for locally unimodal clustering. The method starts with an initial overclustering of the data and relies on the unimodality graph that connects subclusters forming unimodal pairs. Such pairs are identified using an appropriate statistical test. UniForCE identifies maximal locally unimodal clusters by computing a spanning forest in the unimodality graph. Experimental results on both real and synthetic datasets illustrate that the proposed methodology is particularly flexible and robust in discovering regular and highly complex cluster shapes. Most importantly, it automatically provides an adequate estimation of the number of clusters.

A Multivariate Unimodality Test Harnessing the Dip Statistic of Mahalanobis Distances Over Random Projections

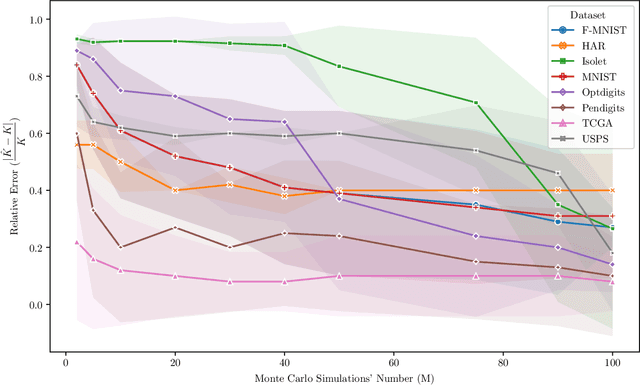
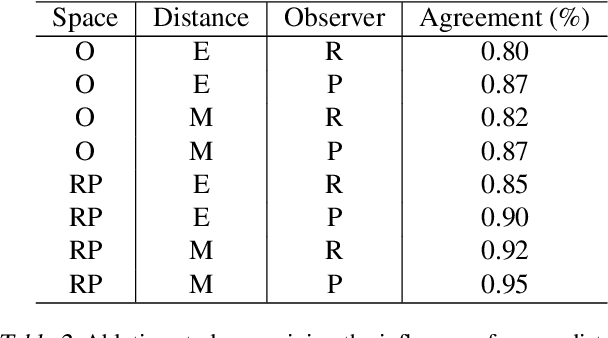
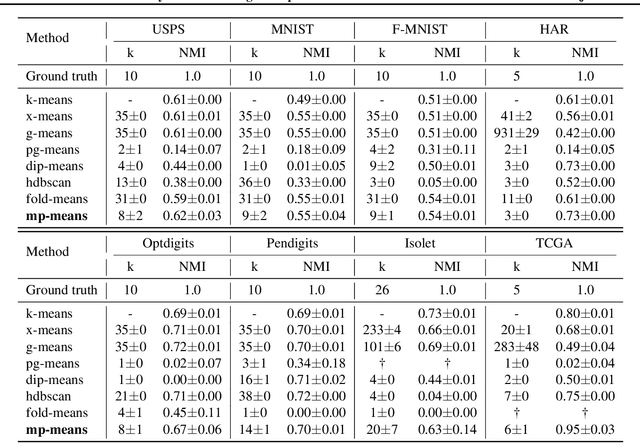
Unimodality, pivotal in statistical analysis, offers insights into dataset structures and drives sophisticated analytical procedures. While unimodality's confirmation is straightforward for one-dimensional data using methods like Silverman's approach and Hartigans' dip statistic, its generalization to higher dimensions remains challenging. By extrapolating one-dimensional unimodality principles to multi-dimensional spaces through linear random projections and leveraging point-to-point distancing, our method, rooted in $\alpha$-unimodality assumptions, presents a novel multivariate unimodality test named mud-pod. Both theoretical and empirical studies confirm the efficacy of our method in unimodality assessment of multidimensional datasets as well as in estimating the number of clusters.

Global $k$-means$++$: an effective relaxation of the global $k$-means clustering algorithm

The $k$-means algorithm is a very prevalent clustering method because of its simplicity, effectiveness, and speed, but its main disadvantage is its high sensitivity to the initial positions of the cluster centers. The global $k$-means is a deterministic algorithm proposed to tackle the random initialization problem of k-means but requires high computational cost. It partitions the data to $K$ clusters by solving all $k$-means sub-problems incrementally for $k=1,\ldots, K$. For each $k$ cluster problem, the method executes the $k$-means algorithm $N$ times, where $N$ is the number of data points. In this paper, we propose the global $k$-means$++$ clustering algorithm, which is an effective way of acquiring quality clustering solutions akin to those of global $k$-means with a reduced computational load. This is achieved by exploiting the center section probability that is used in the effective $k$-means$++$ algorithm. The proposed method has been tested and compared in various well-known real and synthetic datasets yielding very satisfactory results in terms of clustering quality and execution speed.

The UU-test for Statistical Modeling of Unimodal Data

Deciding on the unimodality of a dataset is an important problem in data analysis and statistical modeling. It allows to obtain knowledge about the structure of the dataset, ie. whether data points have been generated by a probability distribution with a single or more than one peaks. Such knowledge is very useful for several data analysis problems, such as for deciding on the number of clusters and determining unimodal projections. We propose a technique called UU-test (Unimodal Uniform test) to decide on the unimodality of a one-dimensional dataset. The method operates on the empirical cumulative density function (ecdf) of the dataset. It attempts to build a piecewise linear approximation of the ecdf that is unimodal and models the data sufficiently in the sense that the data corresponding to each linear segment follows the uniform distribution. A unique feature of this approach is that in the case of unimodality, it also provides a statistical model of the data in the form of a Uniform Mixture Model. We present experimental results in order to assess the ability of the method to decide on unimodality and perform comparisons with the well-known dip-test approach. In addition, in the case of unimodal datasets we evaluate the Uniform Mixture Models provided by the proposed method using the test set log-likelihood and the two-sample Kolmogorov-Smirnov (KS) test.