Geometric Algebra Meets Large Language Models: Instruction-Based Transformations of Separate Meshes in 3D, Interactive and Controllable Scenes

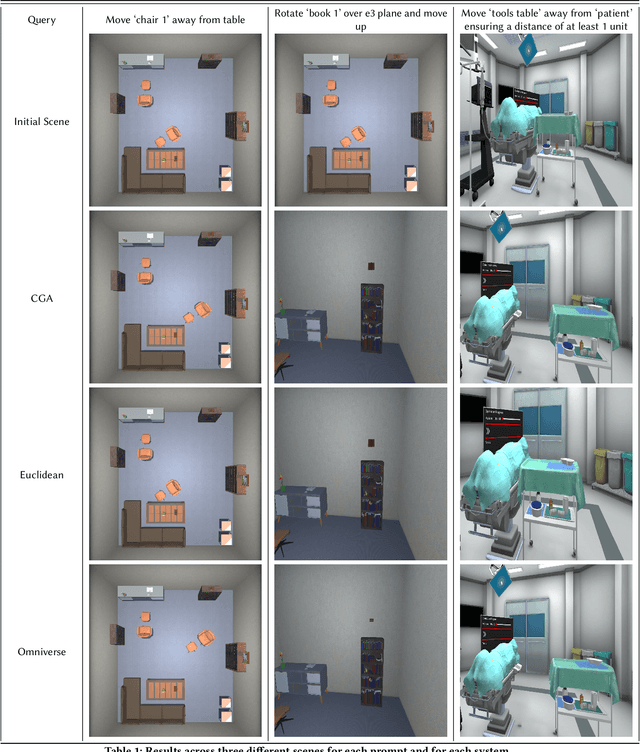
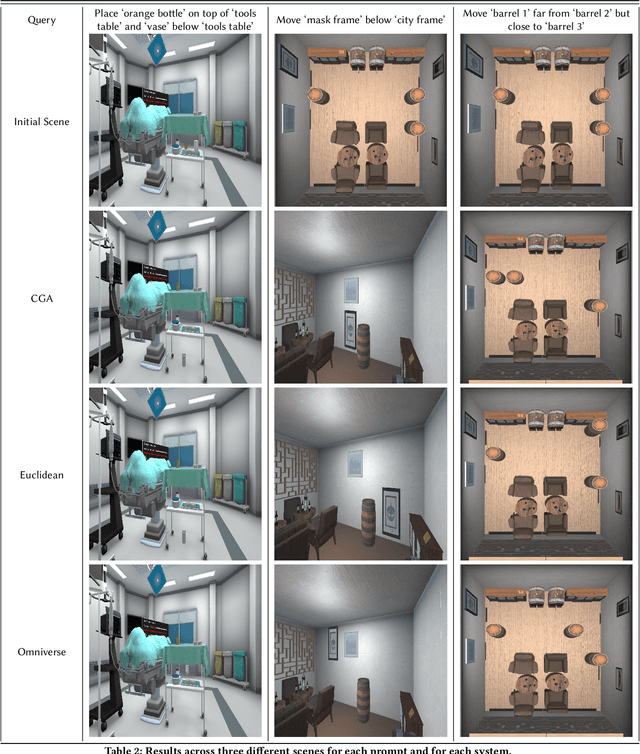
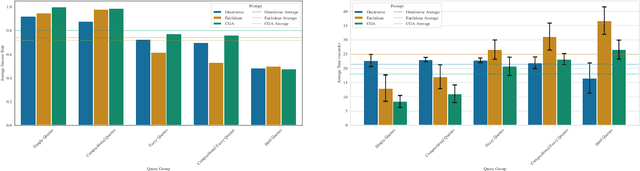
This paper introduces a novel integration of Large Language Models (LLMs) with Conformal Geometric Algebra (CGA) to revolutionize controllable 3D scene editing, particularly for object repositioning tasks, which traditionally requires intricate manual processes and specialized expertise. These conventional methods typically suffer from reliance on large training datasets or lack a formalized language for precise edits. Utilizing CGA as a robust formal language, our system, shenlong, precisely models spatial transformations necessary for accurate object repositioning. Leveraging the zero-shot learning capabilities of pre-trained LLMs, shenlong translates natural language instructions into CGA operations which are then applied to the scene, facilitating exact spatial transformations within 3D scenes without the need for specialized pre-training. Implemented in a realistic simulation environment, shenlong ensures compatibility with existing graphics pipelines. To accurately assess the impact of CGA, we benchmark against robust Euclidean Space baselines, evaluating both latency and accuracy. Comparative performance evaluations indicate that shenlong significantly reduces LLM response times by 16% and boosts success rates by 9.6% on average compared to the traditional methods. Notably, shenlong achieves a 100% perfect success rate in common practical queries, a benchmark where other systems fall short. These advancements underscore shenlong's potential to democratize 3D scene editing, enhancing accessibility and fostering innovation across sectors such as education, digital entertainment, and virtual reality.

A Multivariate Unimodality Test Harnessing the Dip Statistic of Mahalanobis Distances Over Random Projections

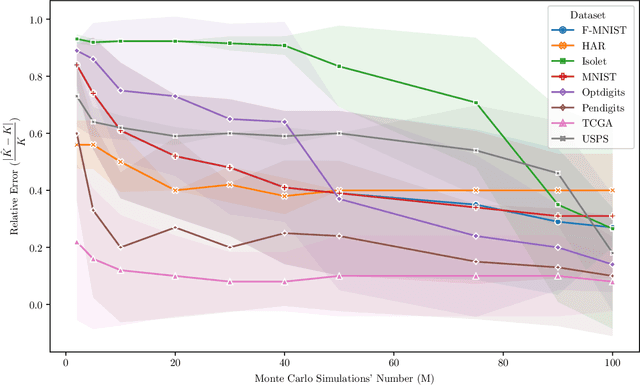
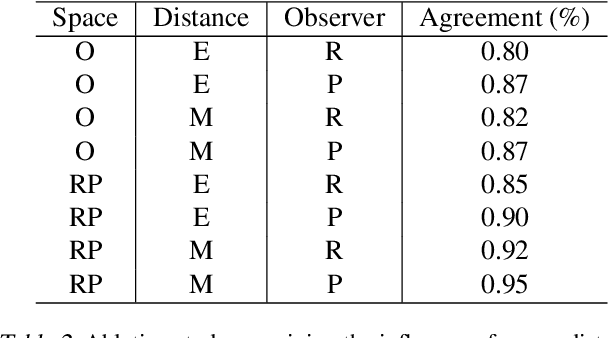
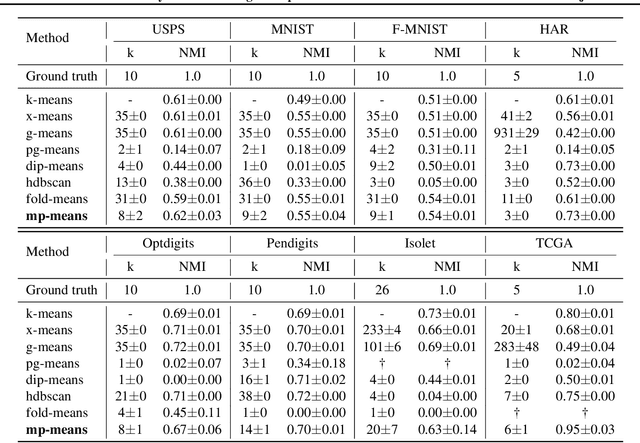
Unimodality, pivotal in statistical analysis, offers insights into dataset structures and drives sophisticated analytical procedures. While unimodality's confirmation is straightforward for one-dimensional data using methods like Silverman's approach and Hartigans' dip statistic, its generalization to higher dimensions remains challenging. By extrapolating one-dimensional unimodality principles to multi-dimensional spaces through linear random projections and leveraging point-to-point distancing, our method, rooted in $\alpha$-unimodality assumptions, presents a novel multivariate unimodality test named mud-pod. Both theoretical and empirical studies confirm the efficacy of our method in unimodality assessment of multidimensional datasets as well as in estimating the number of clusters.

HyperKG: Hyperbolic Knowledge Graph Embeddings for Knowledge Base Completion

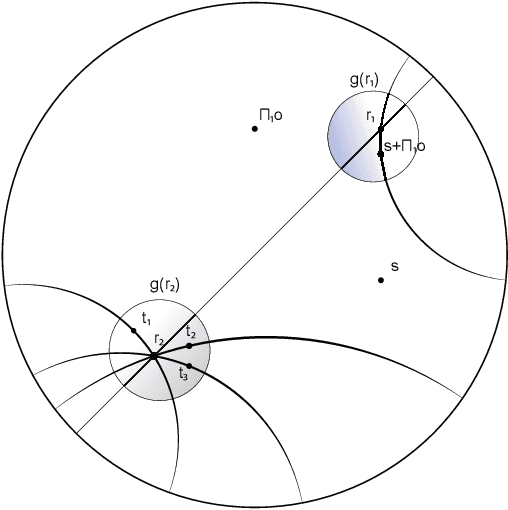
Learning embeddings of entities and relations existing in knowledge bases allows the discovery of hidden patterns in data. In this work, we examine the geometrical space's contribution to the task of knowledge base completion. We focus on the family of translational models, whose performance has been lagging, and propose a model, dubbed HyperKG, which exploits the hyperbolic space in order to better reflect the topological properties of knowledge bases. We investigate the type of regularities that our model can capture and we show that it is a prominent candidate for effectively representing a subset of Datalog rules. We empirically show, using a variety of link prediction datasets, that hyperbolic space allows to narrow down significantly the performance gap between translational and bilinear models.