A Multivariate Unimodality Test Harnessing the Dip Statistic of Mahalanobis Distances Over Random Projections
Paper and Code
Dec 02, 2023
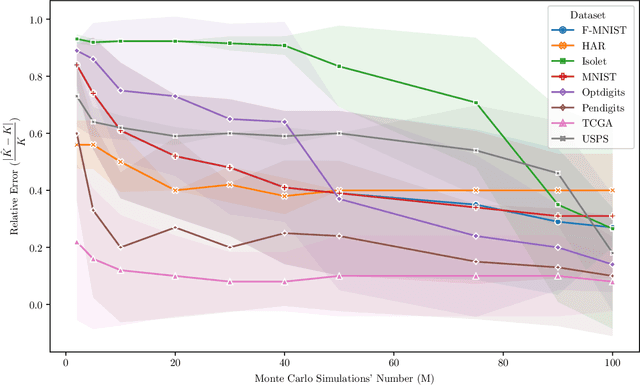
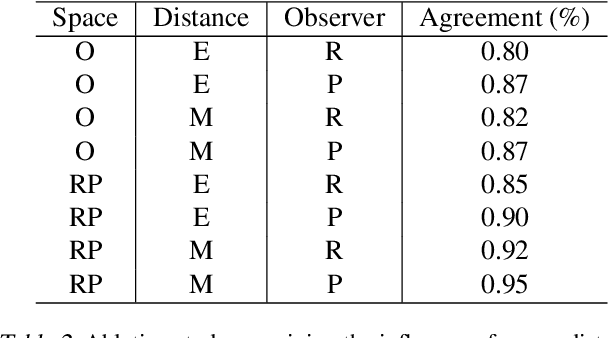
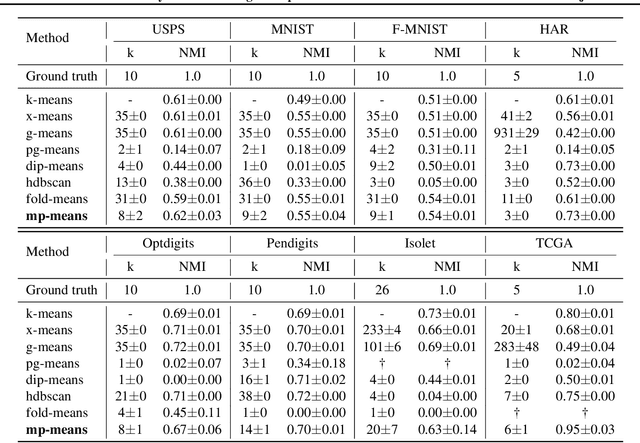
Unimodality, pivotal in statistical analysis, offers insights into dataset structures and drives sophisticated analytical procedures. While unimodality's confirmation is straightforward for one-dimensional data using methods like Silverman's approach and Hartigans' dip statistic, its generalization to higher dimensions remains challenging. By extrapolating one-dimensional unimodality principles to multi-dimensional spaces through linear random projections and leveraging point-to-point distancing, our method, rooted in $\alpha$-unimodality assumptions, presents a novel multivariate unimodality test named mud-pod. Both theoretical and empirical studies confirm the efficacy of our method in unimodality assessment of multidimensional datasets as well as in estimating the number of clusters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge