Collaborative non-parametric two-sample testing

This paper addresses the multiple two-sample test problem in a graph-structured setting, which is a common scenario in fields such as Spatial Statistics and Neuroscience. Each node $v$ in fixed graph deals with a two-sample testing problem between two node-specific probability density functions (pdfs), $p_v$ and $q_v$. The goal is to identify nodes where the null hypothesis $p_v = q_v$ should be rejected, under the assumption that connected nodes would yield similar test outcomes. We propose the non-parametric collaborative two-sample testing (CTST) framework that efficiently leverages the graph structure and minimizes the assumptions over $p_v$ and $q_v$. Our methodology integrates elements from f-divergence estimation, Kernel Methods, and Multitask Learning. We use synthetic experiments and a real sensor network detecting seismic activity to demonstrate that CTST outperforms state-of-the-art non-parametric statistical tests that apply at each node independently, hence disregard the geometry of the problem.

Online non-parametric likelihood-ratio estimation by Pearson-divergence functional minimization

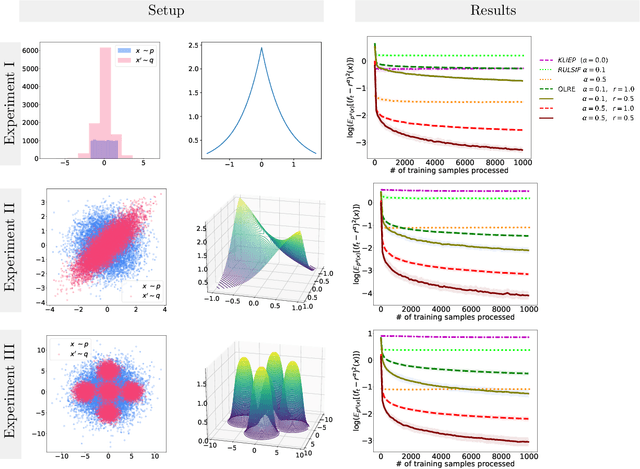
Quantifying the difference between two probability density functions, $p$ and $q$, using available data, is a fundamental problem in Statistics and Machine Learning. A usual approach for addressing this problem is the likelihood-ratio estimation (LRE) between $p$ and $q$, which -- to our best knowledge -- has been investigated mainly for the offline case. This paper contributes by introducing a new framework for online non-parametric LRE (OLRE) for the setting where pairs of iid observations $(x_t \sim p, x'_t \sim q)$ are observed over time. The non-parametric nature of our approach has the advantage of being agnostic to the forms of $p$ and $q$. Moreover, we capitalize on the recent advances in Kernel Methods and functional minimization to develop an estimator that can be efficiently updated online. We provide theoretical guarantees for the performance of the OLRE method along with empirical validation in synthetic experiments.

Online Centralized Non-parametric Change-point Detection via Graph-based Likelihood-ratio Estimation

Consider each node of a graph to be generating a data stream that is synchronized and observed at near real-time. At a change-point $\tau$, a change occurs at a subset of nodes $C$, which affects the probability distribution of their associated node streams. In this paper, we propose a novel kernel-based method to both detect $\tau$ and localize $C$, based on the direct estimation of the likelihood-ratio between the post-change and the pre-change distributions of the node streams. Our main working hypothesis is the smoothness of the likelihood-ratio estimates over the graph, i.e connected nodes are expected to have similar likelihood-ratios. The quality of the proposed method is demonstrated on extensive experiments on synthetic scenarios.

Collaborative likelihood-ratio estimation over graphs

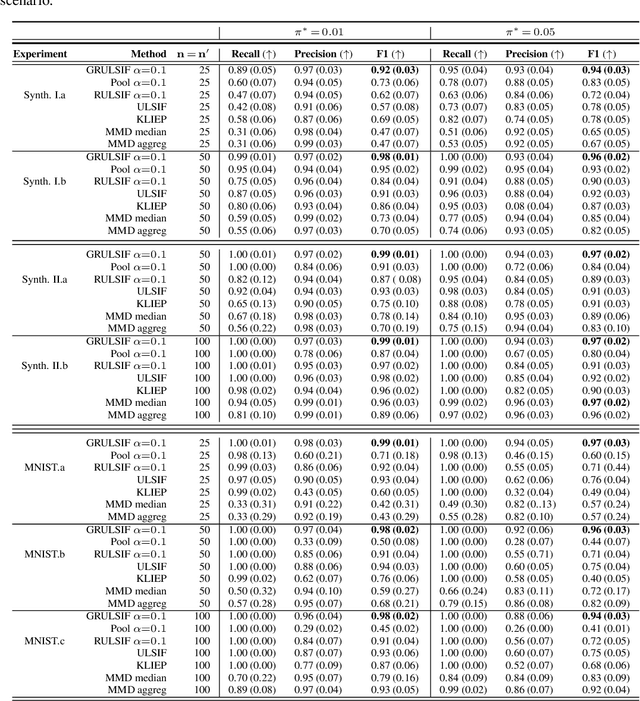
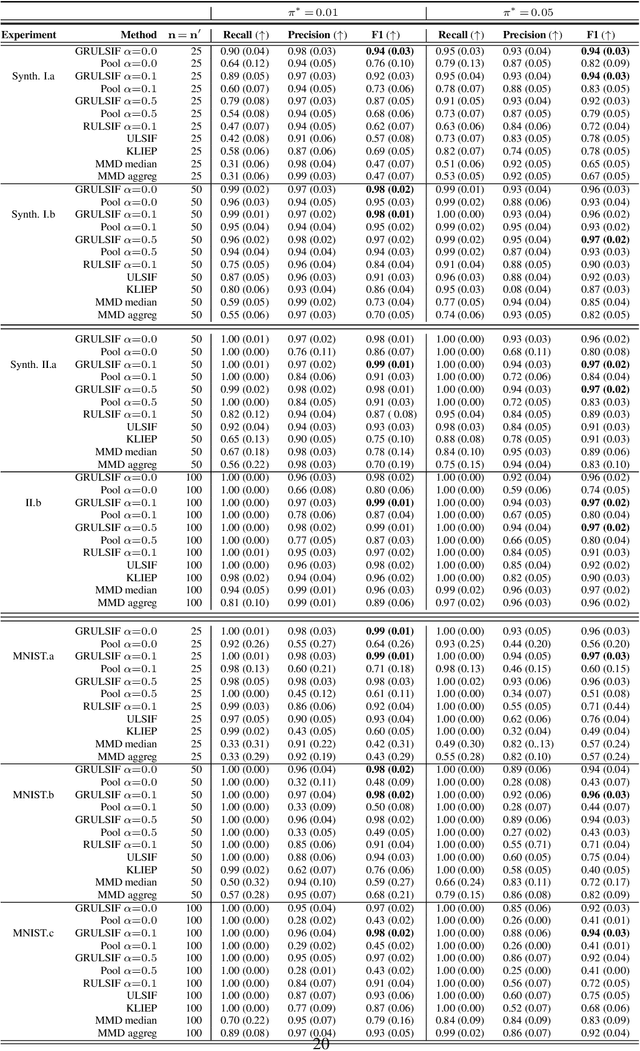
Assuming we have i.i.d observations from two unknown probability density functions (pdfs), $p$ and $p'$, the likelihood-ratio estimation (LRE) is an elegant approach to compare the two pdfs just by relying on the available data, and without knowing the pdfs explicitly. In this paper we introduce a graph-based extension of this problem: Suppose each node $v$ of a fixed graph has access to observations coming from two unknown node-specific pdfs, $p_v$ and $p'_v$; the goal is then to compare the respective $p_v$ and $p'_v$ of each node by also integrating information provided by the graph structure. This setting is interesting when the graph conveys some sort of `similarity' between the node-wise estimation tasks, which suggests that the nodes can collaborate to solve more efficiently their individual tasks, while on the other hand trying to limit the data sharing among them. Our main contribution is a distributed non-parametric framework for graph-based LRE, called GRULSIF, that incorporates in a novel way elements from f-divengence functionals, Kernel methods, and Multitask Learning. Among the several applications of LRE, we choose the two-sample hypothesis testing to develop a proof of concept for our graph-based learning framework. Our experiments compare favorably the performance of our approach against state-of-the-art non-parametric statistical tests that apply at each node independently, and thus disregard the graph structure.

Online non-parametric change-point detection for heterogeneous data streams observed over graph nodes

Consider a heterogeneous data stream being generated by the nodes of a graph. The data stream is in essence composed by multiple streams, possibly of different nature that depends on each node. At a given moment $\tau$, a change-point occurs for a subset of nodes $C$, signifying the change in the probability distribution of their associated streams. In this paper we propose an online non-parametric method to infer $\tau$ based on the direct estimation of the likelihood-ratio between the post-change and the pre-change distribution associated with the data stream of each node. We propose a kernel-based method, under the hypothesis that connected nodes of the graph are expected to have similar likelihood-ratio estimates when there is no change-point. We demonstrate the quality of our method on synthetic experiments and real-world applications.

Offline detection of change-points in the mean for stationary graph signals

This paper addresses the problem of segmenting a stream of graph signals: we aim to detect changes in the mean of the multivariate signal defined over the nodes of a known graph. We propose an offline algorithm that relies on the concept of graph signal stationarity and allows the convenient translation of the problem from the original vertex domain to the spectral domain (Graph Fourier Transform), where it is much easier to solve. Although the obtained spectral representation is sparse in real applications, to the best of our knowledge this property has not been much exploited in the existing related literature. Our main contribution is a change-point detection algorithm that adopts a model selection perspective, which takes into account the sparsity of the spectral representation and determines automatically the number of change-points. Our detector comes with a proof of a non-asymptotic oracle inequality, numerical experiments demonstrate the validity of our method.