Conformal Approach To Gaussian Process Surrogate Evaluation With Coverage Guarantees

Gaussian processes (GPs) are a Bayesian machine learning approach widely used to construct surrogate models for the uncertainty quantification of computer simulation codes in industrial applications. It provides both a mean predictor and an estimate of the posterior prediction variance, the latter being used to produce Bayesian credibility intervals. Interpreting these intervals relies on the Gaussianity of the simulation model as well as the well-specification of the priors which are not always appropriate. We propose to address this issue with the help of conformal prediction. In the present work, a method for building adaptive cross-conformal prediction intervals is proposed by weighting the non-conformity score with the posterior standard deviation of the GP. The resulting conformal prediction intervals exhibit a level of adaptivity akin to Bayesian credibility sets and display a significant correlation with the surrogate model local approximation error, while being free from the underlying model assumptions and having frequentist coverage guarantees. These estimators can thus be used for evaluating the quality of a GP surrogate model and can assist a decision-maker in the choice of the best prior for the specific application of the GP. The performance of the method is illustrated through a panel of numerical examples based on various reference databases. Moreover, the potential applicability of the method is demonstrated in the context of surrogate modeling of an expensive-to-evaluate simulator of the clogging phenomenon in steam generators of nuclear reactors.

dCAM: Dimension-wise Class Activation Map for Explaining Multivariate Data Series Classification

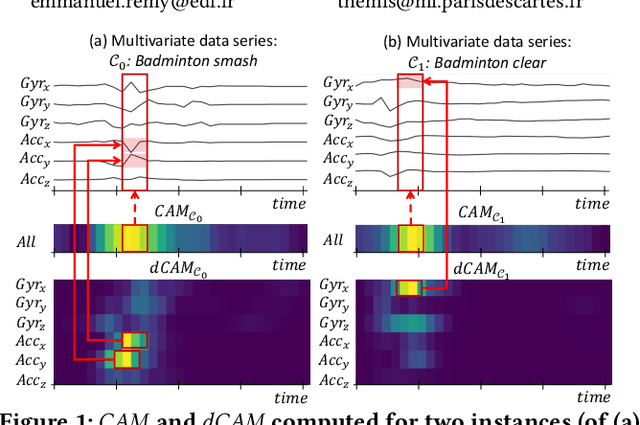
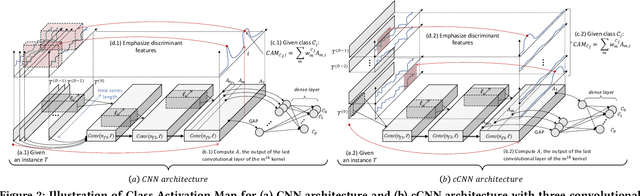
Data series classification is an important and challenging problem in data science. Explaining the classification decisions by finding the discriminant parts of the input that led the algorithm to some decisions is a real need in many applications. Convolutional neural networks perform well for the data series classification task; though, the explanations provided by this type of algorithm are poor for the specific case of multivariate data series. Addressing this important limitation is a significant challenge. In this paper, we propose a novel method that solves this problem by highlighting both the temporal and dimensional discriminant information. Our contribution is two-fold: we first describe a convolutional architecture that enables the comparison of dimensions; then, we propose a method that returns dCAM, a Dimension-wise Class Activation Map specifically designed for multivariate time series (and CNN-based models). Experiments with several synthetic and real datasets demonstrate that dCAM is not only more accurate than previous approaches, but the only viable solution for discriminant feature discovery and classification explanation in multivariate time series. This paper has appeared in SIGMOD'22.