Efficient Precision Control in Object Detection Models for Enhanced and Reliable Ovarian Follicle Counting

Image analysis is a key tool for describing the detailed mechanisms of folliculogenesis, such as evaluating the quantity of mouse Primordial ovarian Follicles (PMF) in the ovarian reserve. The development of high-resolution virtual slide scanners offers the possibility of quantifying, robustifying and accelerating the histopathological procedure. A major challenge for machine learning is to control the precision of predictions while enabling a high recall, in order to provide reproducibility. We use a multiple testing procedure that gives an overperforming way to solve the standard Precision-Recall trade-off that gives probabilistic guarantees on the precision. In addition, we significantly improve the overall performance of the models (increase of F1-score) by selecting the decision threshold using contextual biological information or using an auxiliary model. As it is model-agnostic, this contextual selection procedure paves the way to the development of a strategy that can improve the performance of any model without the need of retraining it.

Automatically Adaptive Conformal Risk Control

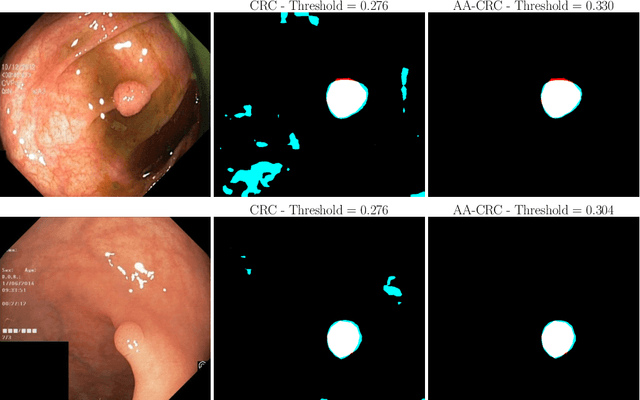
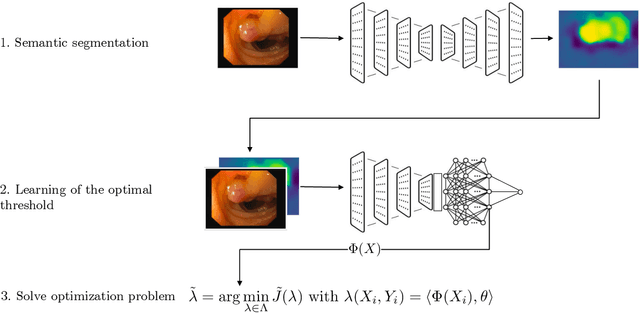
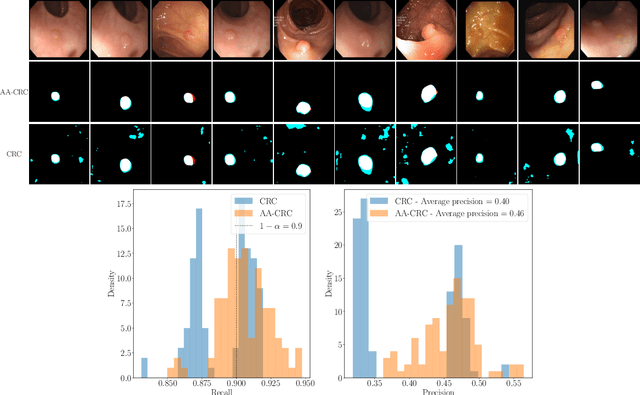
Science and technology have a growing need for effective mechanisms that ensure reliable, controlled performance from black-box machine learning algorithms. These performance guarantees should ideally hold conditionally on the input-that is the performance guarantees should hold, at least approximately, no matter what the input. However, beyond stylized discrete groupings such as ethnicity and gender, the right notion of conditioning can be difficult to define. For example, in problems such as image segmentation, we want the uncertainty to reflect the intrinsic difficulty of the test sample, but this may be difficult to capture via a conditioning event. Building on the recent work of Gibbs et al. [2023], we propose a methodology for achieving approximate conditional control of statistical risks-the expected value of loss functions-by adapting to the difficulty of test samples. Our framework goes beyond traditional conditional risk control based on user-provided conditioning events to the algorithmic, data-driven determination of appropriate function classes for conditioning. We apply this framework to various regression and segmentation tasks, enabling finer-grained control over model performance and demonstrating that by continuously monitoring and adjusting these parameters, we can achieve superior precision compared to conventional risk-control methods.

Conformal Approach To Gaussian Process Surrogate Evaluation With Coverage Guarantees

Gaussian processes (GPs) are a Bayesian machine learning approach widely used to construct surrogate models for the uncertainty quantification of computer simulation codes in industrial applications. It provides both a mean predictor and an estimate of the posterior prediction variance, the latter being used to produce Bayesian credibility intervals. Interpreting these intervals relies on the Gaussianity of the simulation model as well as the well-specification of the priors which are not always appropriate. We propose to address this issue with the help of conformal prediction. In the present work, a method for building adaptive cross-conformal prediction intervals is proposed by weighting the non-conformity score with the posterior standard deviation of the GP. The resulting conformal prediction intervals exhibit a level of adaptivity akin to Bayesian credibility sets and display a significant correlation with the surrogate model local approximation error, while being free from the underlying model assumptions and having frequentist coverage guarantees. These estimators can thus be used for evaluating the quality of a GP surrogate model and can assist a decision-maker in the choice of the best prior for the specific application of the GP. The performance of the method is illustrated through a panel of numerical examples based on various reference databases. Moreover, the potential applicability of the method is demonstrated in the context of surrogate modeling of an expensive-to-evaluate simulator of the clogging phenomenon in steam generators of nuclear reactors.

MAPIE: an open-source library for distribution-free uncertainty quantification

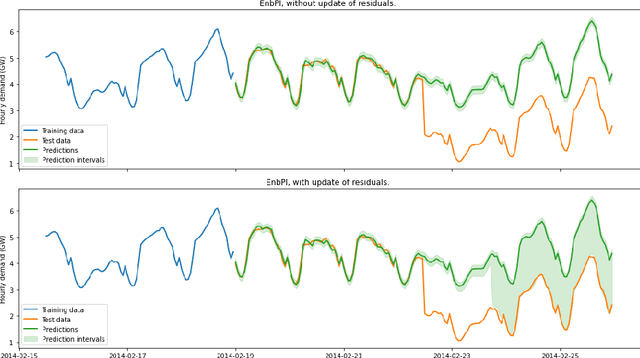
Estimating uncertainties associated with the predictions of Machine Learning (ML) models is of crucial importance to assess their robustness and predictive power. In this submission, we introduce MAPIE (Model Agnostic Prediction Interval Estimator), an open-source Python library that quantifies the uncertainties of ML models for single-output regression and multi-class classification tasks. MAPIE implements conformal prediction methods, allowing the user to easily compute uncertainties with strong theoretical guarantees on the marginal coverages and with mild assumptions on the model or on the underlying data distribution. MAPIE is hosted on scikit-learn-contrib and is fully "scikit-learn-compatible". As such, it accepts any type of regressor or classifier coming with a scikit-learn API. The library is available at: https://github.com/scikit-learn-contrib/MAPIE/.