ToolFlood: Beyond Selection -- Hiding Valid Tools from LLM Agents via Semantic Covering

Large Language Model (LLM) agents increasingly use external tools for complex tasks and rely on embedding-based retrieval to select a small top-k subset for reasoning. As these systems scale, the robustness of this retrieval stage is underexplored, even though prior work has examined attacks on tool selection. This paper introduces ToolFlood, a retrieval-layer attack on tool-augmented LLM agents. Rather than altering which tool is chosen after retrieval, ToolFlood overwhelms retrieval itself by injecting a few attacker-controlled tools whose metadata is carefully placed by exploiting the geometry of embedding space. These tools semantically span many user queries, dominate the top-k results, and push all benign tools out of the agent's context. ToolFlood uses a two-phase adversarial tool generation strategy. It first samples subsets of target queries and uses an LLM to iteratively generate diverse tool names and descriptions. It then runs an iterative greedy selection that chooses tools maximizing coverage of remaining queries in embedding space under a cosine-distance threshold, stopping when all queries are covered or a budget is reached. We provide theoretical analysis of retrieval saturation and show on standard benchmarks that ToolFlood achieves up to a 95% attack success rate with a low injection rate (1% in ToolBench). The code will be made publicly available at the following link: https://github.com/as1-prog/ToolFlood

Automatically Adaptive Conformal Risk Control

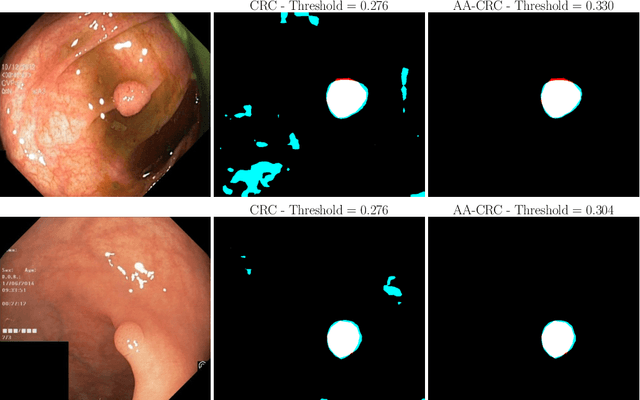
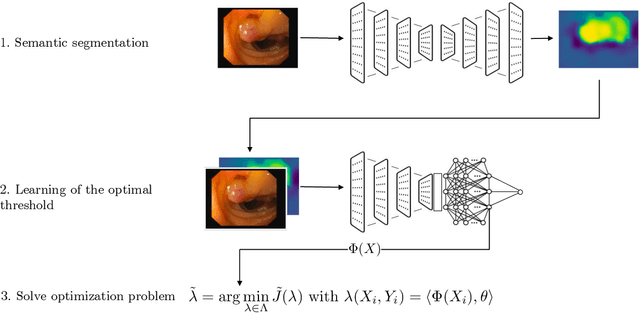
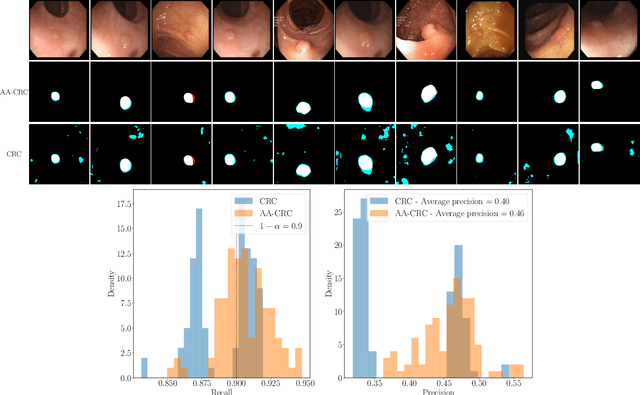
Science and technology have a growing need for effective mechanisms that ensure reliable, controlled performance from black-box machine learning algorithms. These performance guarantees should ideally hold conditionally on the input-that is the performance guarantees should hold, at least approximately, no matter what the input. However, beyond stylized discrete groupings such as ethnicity and gender, the right notion of conditioning can be difficult to define. For example, in problems such as image segmentation, we want the uncertainty to reflect the intrinsic difficulty of the test sample, but this may be difficult to capture via a conditioning event. Building on the recent work of Gibbs et al. [2023], we propose a methodology for achieving approximate conditional control of statistical risks-the expected value of loss functions-by adapting to the difficulty of test samples. Our framework goes beyond traditional conditional risk control based on user-provided conditioning events to the algorithmic, data-driven determination of appropriate function classes for conditioning. We apply this framework to various regression and segmentation tasks, enabling finer-grained control over model performance and demonstrating that by continuously monitoring and adjusting these parameters, we can achieve superior precision compared to conventional risk-control methods.