Nicolas Brunel
The State of the Art AI company, ENSIIE
Weighted Conformal Prediction Provides Adaptive and Valid Mask-Conditional Coverage for General Missing Data Mechanisms
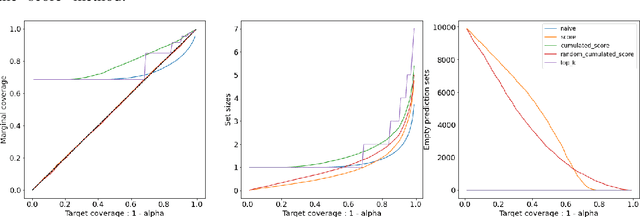
Dec 16, 2025Abstract:Conformal prediction (CP) offers a principled framework for uncertainty quantification, but it fails to guarantee coverage when faced with missing covariates. In addressing the heterogeneity induced by various missing patterns, Mask-Conditional Valid (MCV) Coverage has emerged as a more desirable property than Marginal Coverage. In this work, we adapt split CP to handle missing values by proposing a preimpute-mask-then-correct framework that can offer valid coverage. We show that our method provides guaranteed Marginal Coverage and Mask-Conditional Validity for general missing data mechanisms. A key component of our approach is a reweighted conformal prediction procedure that corrects the prediction sets after distributional imputation (multiple imputation) of the calibration dataset, making our method compatible with standard imputation pipelines. We derive two algorithms, and we show that they are approximately marginally valid and MCV. We evaluate them on synthetic and real-world datasets. It reduces significantly the width of prediction intervals w.r.t standard MCV methods, while maintaining the target guarantees.
Conformal Approach To Gaussian Process Surrogate Evaluation With Coverage Guarantees
Jan 15, 2024Abstract:Gaussian processes (GPs) are a Bayesian machine learning approach widely used to construct surrogate models for the uncertainty quantification of computer simulation codes in industrial applications. It provides both a mean predictor and an estimate of the posterior prediction variance, the latter being used to produce Bayesian credibility intervals. Interpreting these intervals relies on the Gaussianity of the simulation model as well as the well-specification of the priors which are not always appropriate. We propose to address this issue with the help of conformal prediction. In the present work, a method for building adaptive cross-conformal prediction intervals is proposed by weighting the non-conformity score with the posterior standard deviation of the GP. The resulting conformal prediction intervals exhibit a level of adaptivity akin to Bayesian credibility sets and display a significant correlation with the surrogate model local approximation error, while being free from the underlying model assumptions and having frequentist coverage guarantees. These estimators can thus be used for evaluating the quality of a GP surrogate model and can assist a decision-maker in the choice of the best prior for the specific application of the GP. The performance of the method is illustrated through a panel of numerical examples based on various reference databases. Moreover, the potential applicability of the method is demonstrated in the context of surrogate modeling of an expensive-to-evaluate simulator of the clogging phenomenon in steam generators of nuclear reactors.
Robust PCA for Anomaly Detection and Data Imputation in Seasonal Time Series
Aug 03, 2022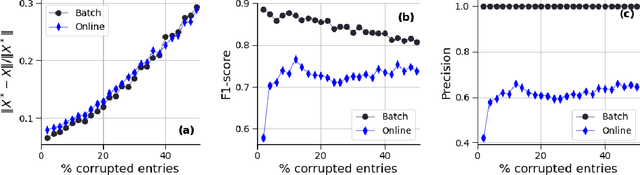
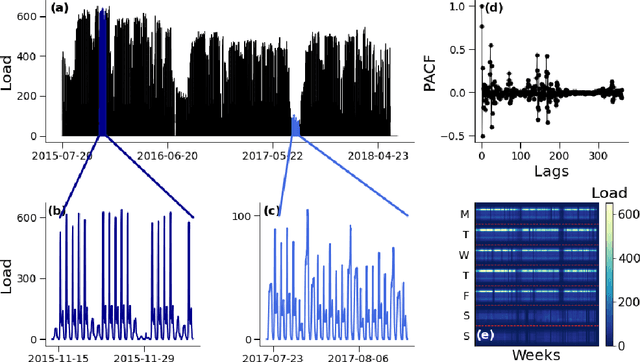
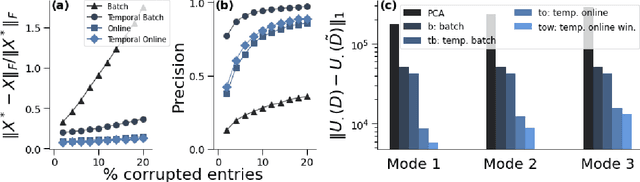
Abstract:We propose a robust principal component analysis (RPCA) framework to recover low-rank and sparse matrices from temporal observations. We develop an online version of the batch temporal algorithm in order to process larger datasets or streaming data. We empirically compare the proposed approaches with different RPCA frameworks and show their effectiveness in practical situations.
MAPIE: an open-source library for distribution-free uncertainty quantification
Jul 25, 2022
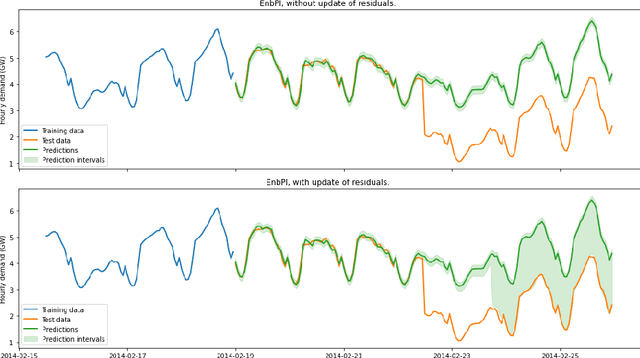
Abstract:Estimating uncertainties associated with the predictions of Machine Learning (ML) models is of crucial importance to assess their robustness and predictive power. In this submission, we introduce MAPIE (Model Agnostic Prediction Interval Estimator), an open-source Python library that quantifies the uncertainties of ML models for single-output regression and multi-class classification tasks. MAPIE implements conformal prediction methods, allowing the user to easily compute uncertainties with strong theoretical guarantees on the marginal coverages and with mild assumptions on the model or on the underlying data distribution. MAPIE is hosted on scikit-learn-contrib and is fully "scikit-learn-compatible". As such, it accepts any type of regressor or classifier coming with a scikit-learn API. The library is available at: https://github.com/scikit-learn-contrib/MAPIE/.
Bayesian reconstruction of memories stored in neural networks from their connectivity
May 16, 2021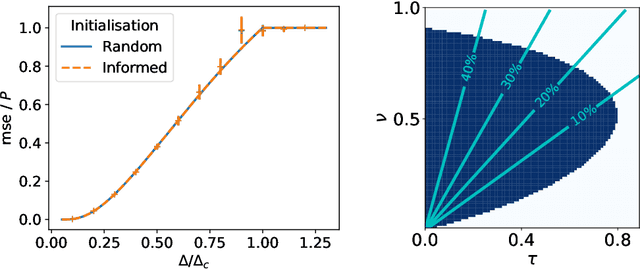
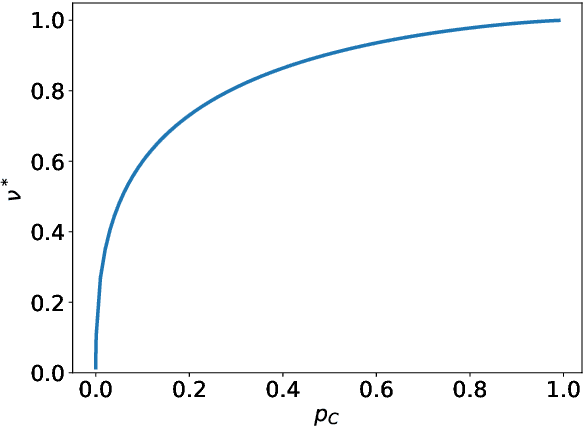
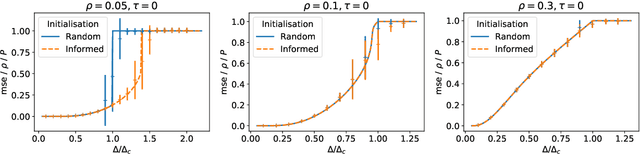
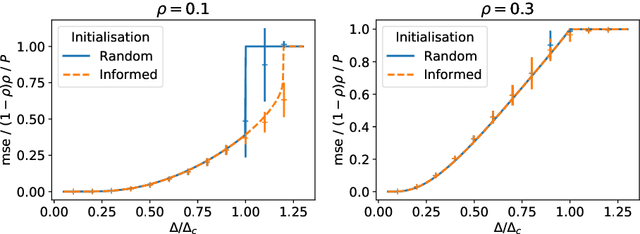
Abstract:The advent of comprehensive synaptic wiring diagrams of large neural circuits has created the field of connectomics and given rise to a number of open research questions. One such question is whether it is possible to reconstruct the information stored in a recurrent network of neurons, given its synaptic connectivity matrix. Here, we address this question by determining when solving such an inference problem is theoretically possible in specific attractor network models and by providing a practical algorithm to do so. The algorithm builds on ideas from statistical physics to perform approximate Bayesian inference and is amenable to exact analysis. We study its performance on three different models and explore the limitations of reconstructing stored patterns from synaptic connectivity.
Efficient supervised learning in networks with binary synapses
Jul 09, 2007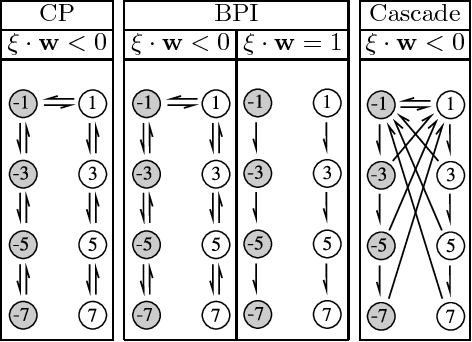

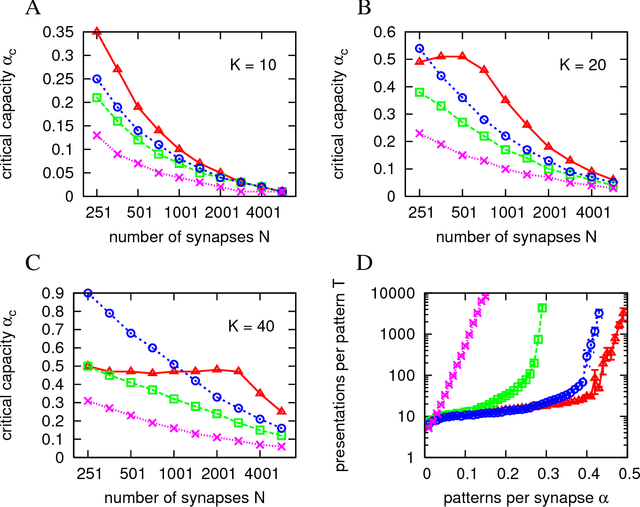
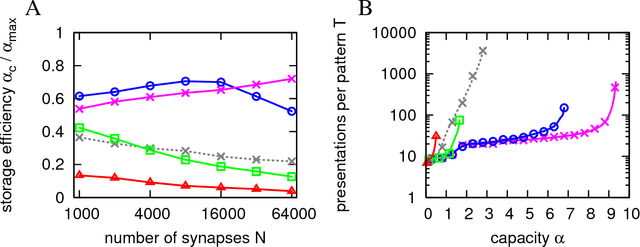
Abstract:Recent experimental studies indicate that synaptic changes induced by neuronal activity are discrete jumps between a small number of stable states. Learning in systems with discrete synapses is known to be a computationally hard problem. Here, we study a neurobiologically plausible on-line learning algorithm that derives from Belief Propagation algorithms. We show that it performs remarkably well in a model neuron with binary synapses, and a finite number of `hidden' states per synapse, that has to learn a random classification task. Such system is able to learn a number of associations close to the theoretical limit, in time which is sublinear in system size. This is to our knowledge the first on-line algorithm that is able to achieve efficiently a finite number of patterns learned per binary synapse. Furthermore, we show that performance is optimal for a finite number of hidden states which becomes very small for sparse coding. The algorithm is similar to the standard `perceptron' learning algorithm, with an additional rule for synaptic transitions which occur only if a currently presented pattern is `barely correct'. In this case, the synaptic changes are meta-plastic only (change in hidden states and not in actual synaptic state), stabilizing the synapse in its current state. Finally, we show that a system with two visible states and K hidden states is much more robust to noise than a system with K visible states. We suggest this rule is sufficiently simple to be easily implemented by neurobiological systems or in hardware.
* 10 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge