Efficient supervised learning in networks with binary synapses
Paper and Code
Jul 09, 2007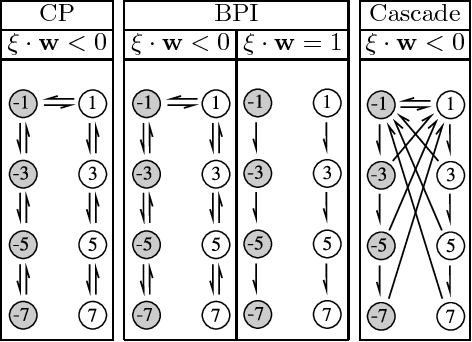

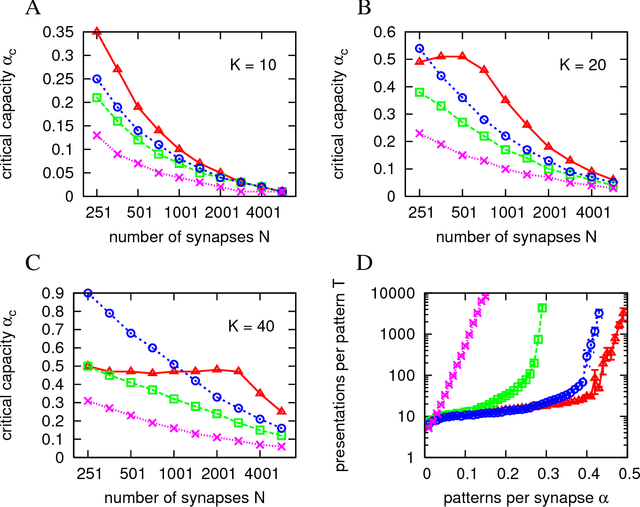
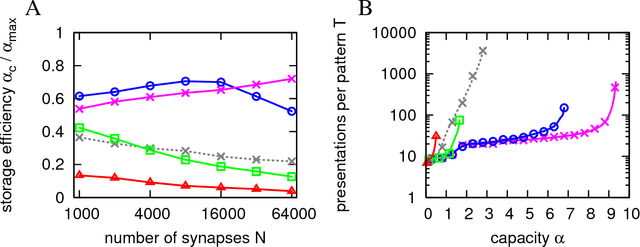
Recent experimental studies indicate that synaptic changes induced by neuronal activity are discrete jumps between a small number of stable states. Learning in systems with discrete synapses is known to be a computationally hard problem. Here, we study a neurobiologically plausible on-line learning algorithm that derives from Belief Propagation algorithms. We show that it performs remarkably well in a model neuron with binary synapses, and a finite number of `hidden' states per synapse, that has to learn a random classification task. Such system is able to learn a number of associations close to the theoretical limit, in time which is sublinear in system size. This is to our knowledge the first on-line algorithm that is able to achieve efficiently a finite number of patterns learned per binary synapse. Furthermore, we show that performance is optimal for a finite number of hidden states which becomes very small for sparse coding. The algorithm is similar to the standard `perceptron' learning algorithm, with an additional rule for synaptic transitions which occur only if a currently presented pattern is `barely correct'. In this case, the synaptic changes are meta-plastic only (change in hidden states and not in actual synaptic state), stabilizing the synapse in its current state. Finally, we show that a system with two visible states and K hidden states is much more robust to noise than a system with K visible states. We suggest this rule is sufficiently simple to be easily implemented by neurobiological systems or in hardware.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge