Geometry-aware framework for deep energy method: an application to structural mechanics with hyperelastic materials

Physics-Informed Neural Networks (PINNs) have gained considerable interest in diverse engineering domains thanks to their capacity to integrate physical laws into deep learning models. Recently, geometry-aware PINN-based approaches that employ the strong form of underlying physical system equations have been developed with the aim of integrating geometric information into PINNs. Despite ongoing research, the assessment of PINNs in problems with various geometries remains an active area of investigation. In this work, we introduce a novel physics-informed framework named the Geometry-Aware Deep Energy Method (GADEM) for solving structural mechanics problems on different geometries. As the weak form of the physical system equation (or the energy-based approach) has demonstrated clear advantages compared to the strong form for solving solid mechanics problems, GADEM employs the weak form and aims to infer the solution on multiple shapes of geometries. Integrating a geometry-aware framework into an energy-based method results in an effective physics-informed deep learning model in terms of accuracy and computational cost. Different ways to represent the geometric information and to encode the geometric latent vectors are investigated in this work. We introduce a loss function of GADEM which is minimized based on the potential energy of all considered geometries. An adaptive learning method is also employed for the sampling of collocation points to enhance the performance of GADEM. We present some applications of GADEM to solve solid mechanics problems, including a loading simulation of a toy tire involving contact mechanics and large deformation hyperelasticity. The numerical results of this work demonstrate the remarkable capability of GADEM to infer the solution on various and new shapes of geometries using only one trained model.

Fixed-budget online adaptive mesh learning for physics-informed neural networks. Towards parameterized problem inference

Physics-Informed Neural Networks (PINNs) have gained much attention in various fields of engineering thanks to their capability of incorporating physical laws into the models. PINNs integrate the physical constraints by minimizing the partial differential equations (PDEs) residuals on a set of collocation points. The distribution of these collocation points appears to have a huge impact on the performance of PINNs and the assessment of the sampling methods for these points is still an active topic. In this paper, we propose a Fixed-Budget Online Adaptive Mesh Learning (FBOAML) method, which decomposes the domain into sub-domains, for training collocation points based on local maxima and local minima of the PDEs residuals. The stopping criterion is based on a data set of reference, which leads to an adaptive number of iterations for each specific problem. The effectiveness of FBOAML is demonstrated in the context of non-parameterized and parameterized problems. The impact of the hyper-parameters in FBOAML is investigated in this work. The comparison with other adaptive sampling methods is also illustrated. The numerical results demonstrate important gains in terms of accuracy of PINNs with FBOAML over the classical PINNs with non-adaptive collocation points. We also apply FBOAML in a complex industrial application involving coupling between mechanical and thermal fields. We show that FBOAML is able to identify the high-gradient location and even give better prediction for some physical fields than the classical PINNs with collocation points taken on a pre-adapted finite element mesh.

Continuous Methods : Adaptively intrusive reduced order model closure

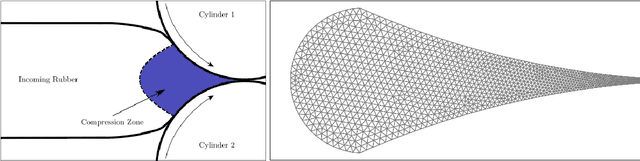
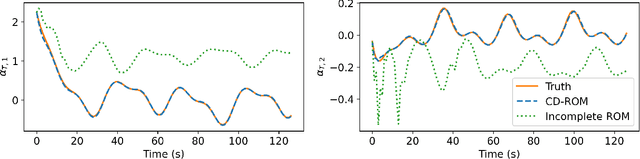
Reduced order modeling methods are often used as a mean to reduce simulation costs in industrial applications. Despite their computational advantages, reduced order models (ROMs) often fail to accurately reproduce complex dynamics encountered in real life applications. To address this challenge, we leverage NeuralODEs to propose a novel ROM correction approach based on a time-continuous memory formulation. Finally, experimental results show that our proposed method provides a high level of accuracy while retaining the low computational costs inherent to reduced models.

Physics-informed neural networks for non-Newtonian fluid thermo-mechanical problems: an application to rubber calendering process

Physics-Informed Neural Networks (PINNs) have gained much attention in various fields of engineering thanks to their capability of incorporating physical laws into the models. However, the assessment of PINNs in industrial applications involving coupling between mechanical and thermal fields is still an active research topic. In this work, we present an application of PINNs to a non-Newtonian fluid thermo-mechanical problem which is often considered in the rubber calendering process. We demonstrate the effectiveness of PINNs when dealing with inverse and ill-posed problems, which are impractical to be solved by classical numerical discretization methods. We study the impact of the placement of the sensors and the distribution of unsupervised points on the performance of PINNs in a problem of inferring hidden physical fields from some partial data. We also investigate the capability of PINNs to identify unknown physical parameters from the measurements captured by sensors. The effect of noisy measurements is also considered throughout this work. The results of this paper demonstrate that in the problem of identification, PINNs can successfully estimate the unknown parameters using only the measurements on the sensors. In ill-posed problems where boundary conditions are not completely defined, even though the placement of the sensors and the distribution of unsupervised points have a great impact on PINNs performance, we show that the algorithm is able to infer the hidden physics from local measurements.