Physics-Learning AI Datamodel (PLAID) datasets: a collection of physics simulations for machine learning

Machine learning-based surrogate models have emerged as a powerful tool to accelerate simulation-driven scientific workflows. However, their widespread adoption is hindered by the lack of large-scale, diverse, and standardized datasets tailored to physics-based simulations. While existing initiatives provide valuable contributions, many are limited in scope-focusing on specific physics domains, relying on fragmented tooling, or adhering to overly simplistic datamodels that restrict generalization. To address these limitations, we introduce PLAID (Physics-Learning AI Datamodel), a flexible and extensible framework for representing and sharing datasets of physics simulations. PLAID defines a unified standard for describing simulation data and is accompanied by a library for creating, reading, and manipulating complex datasets across a wide range of physical use cases (gitlab.com/drti/plaid). We release six carefully crafted datasets under the PLAID standard, covering structural mechanics and computational fluid dynamics, and provide baseline benchmarks using representative learning methods. Benchmarking tools are made available on Hugging Face, enabling direct participation by the community and contribution to ongoing evaluation efforts (huggingface.co/PLAIDcompetitions).

Multi-Level GNN Preconditioner for Solving Large Scale Problems

Large-scale numerical simulations often come at the expense of daunting computations. High-Performance Computing has enhanced the process, but adapting legacy codes to leverage parallel GPU computations remains challenging. Meanwhile, Machine Learning models can harness GPU computations effectively but often struggle with generalization and accuracy. Graph Neural Networks (GNNs), in particular, are great for learning from unstructured data like meshes but are often limited to small-scale problems. Moreover, the capabilities of the trained model usually restrict the accuracy of the data-driven solution. To benefit from both worlds, this paper introduces a novel preconditioner integrating a GNN model within a multi-level Domain Decomposition framework. The proposed GNN-based preconditioner is used to enhance the efficiency of a Krylov method, resulting in a hybrid solver that can converge with any desired level of accuracy. The efficiency of the Krylov method greatly benefits from the GNN preconditioner, which is adaptable to meshes of any size and shape, is executed on GPUs, and features a multi-level approach to enforce the scalability of the entire process. Several experiments are conducted to validate the numerical behavior of the hybrid solver, and an in-depth analysis of its performance is proposed to assess its competitiveness against a C++ legacy solver.

Enhancing Data-Assimilation in CFD using Graph Neural Networks

We present a novel machine learning approach for data assimilation applied in fluid mechanics, based on adjoint-optimization augmented by Graph Neural Networks (GNNs) models. We consider as baseline the Reynolds-Averaged Navier-Stokes (RANS) equations, where the unknown is the meanflow and a closure model based on the Reynolds-stress tensor is required for correctly computing the solution. An end-to-end process is cast; first, we train a GNN model for the closure term. Second, the GNN model is introduced in the training process of data assimilation, where the RANS equations act as a physics constraint for a consistent prediction. We obtain our results using direct numerical simulations based on a Finite Element Method (FEM) solver; a two-fold interface between the GNN model and the solver allows the GNN's predictions to be incorporated into post-processing steps of the FEM analysis. The proposed scheme provides an excellent reconstruction of the meanflow without any features selection; preliminary results show promising generalization properties over unseen flow configurations.

Continuous Methods : Adaptively intrusive reduced order model closure

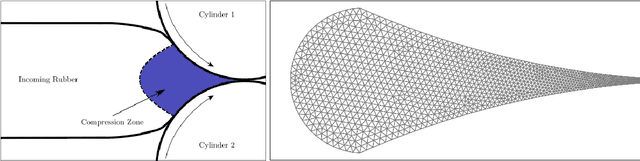
Reduced order modeling methods are often used as a mean to reduce simulation costs in industrial applications. Despite their computational advantages, reduced order models (ROMs) often fail to accurately reproduce complex dynamics encountered in real life applications. To address this challenge, we leverage NeuralODEs to propose a novel ROM correction approach based on a time-continuous memory formulation. Finally, experimental results show that our proposed method provides a high level of accuracy while retaining the low computational costs inherent to reduced models.

Continuous Methods : Hamiltonian Domain Translation

This paper proposes a novel approach to domain translation. Leveraging established parallels between generative models and dynamical systems, we propose a reformulation of the Cycle-GAN architecture. By embedding our model with a Hamiltonian structure, we obtain a continuous, expressive and most importantly invertible generative model for domain translation.

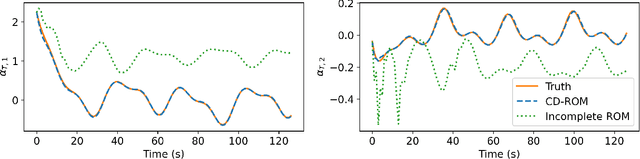
CD-ROM: Complementary Deep-Reduced Order Model

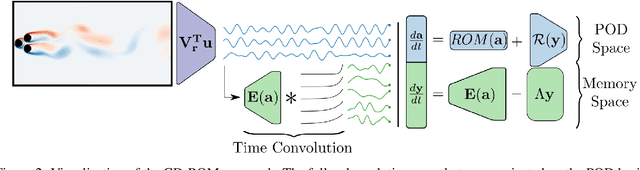
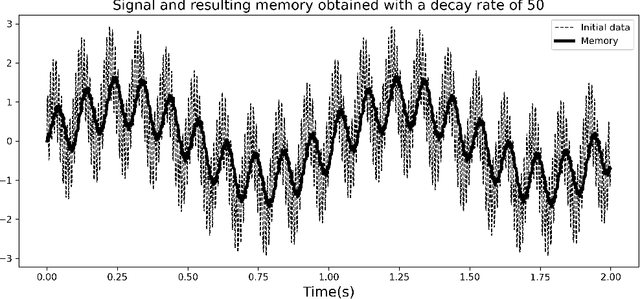
Model order reduction through the POD-Galerkin method can lead to dramatic gains in terms of computational efficiency in solving physical problems. However, the applicability of the method to non linear high-dimensional dynamical systems such as the Navier-Stokes equations has been shown to be limited, producing inaccurate and sometimes unstable models. This paper proposes a closure modeling approach for classical POD-Galerkin reduced order models (ROM). We use multi layer perceptrons (MLP) to learn a continuous in time closure model through the recently proposed Neural ODE method. Inspired by Taken's theorem as well as the Mori-Zwanzig formalism, we augment ROMs with a delay differential equation architecture to model non-Markovian effects in reduced models. The proposed model, called CD-ROM (Complementary Deep-Reduced Order Model) is able to retain information from past states of the system and use it to correct the imperfect reduced dynamics. The model can be integrated in time as a system of ordinary differential equations using any classical time marching scheme. We demonstrate the ability of our CD-ROM approach to improve the accuracy of POD-Galerkin models on two CFD examples, even in configurations unseen during training.