CD-ROM: Complementary Deep-Reduced Order Model
Paper and Code
Mar 10, 2022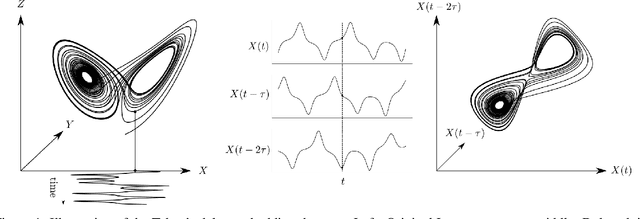

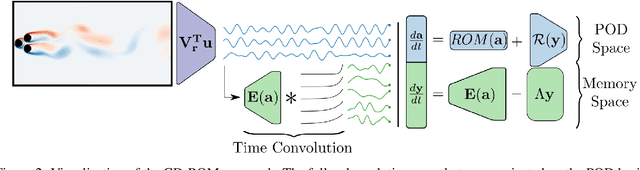
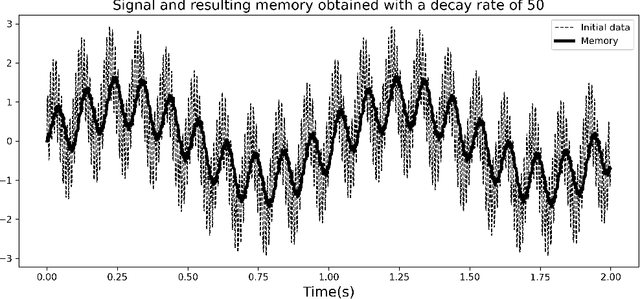
Model order reduction through the POD-Galerkin method can lead to dramatic gains in terms of computational efficiency in solving physical problems. However, the applicability of the method to non linear high-dimensional dynamical systems such as the Navier-Stokes equations has been shown to be limited, producing inaccurate and sometimes unstable models. This paper proposes a closure modeling approach for classical POD-Galerkin reduced order models (ROM). We use multi layer perceptrons (MLP) to learn a continuous in time closure model through the recently proposed Neural ODE method. Inspired by Taken's theorem as well as the Mori-Zwanzig formalism, we augment ROMs with a delay differential equation architecture to model non-Markovian effects in reduced models. The proposed model, called CD-ROM (Complementary Deep-Reduced Order Model) is able to retain information from past states of the system and use it to correct the imperfect reduced dynamics. The model can be integrated in time as a system of ordinary differential equations using any classical time marching scheme. We demonstrate the ability of our CD-ROM approach to improve the accuracy of POD-Galerkin models on two CFD examples, even in configurations unseen during training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge