Evidence on the Regularisation Properties of Maximum-Entropy Reinforcement Learning

The generalisation and robustness properties of policies learnt through Maximum-Entropy Reinforcement Learning are investigated on chaotic dynamical systems with Gaussian noise on the observable. First, the robustness under noise contamination of the agent's observation of entropy regularised policies is observed. Second, notions of statistical learning theory, such as complexity measures on the learnt model, are borrowed to explain and predict the phenomenon. Results show the existence of a relationship between entropy-regularised policy optimisation and robustness to noise, which can be described by the chosen complexity measures.

Increasing Information for Model Predictive Control with Semi-Markov Decision Processes

Recent works in Learning-Based Model Predictive Control of dynamical systems show impressive sample complexity performances using criteria from Information Theory to accelerate the learning procedure. However, the sequential exploration opportunities are limited by the system local state, restraining the amount of information of the observations from the current exploration trajectory. This article resolves this limitation by introducing temporal abstraction through the framework of Semi-Markov Decision Processes. The framework increases the total information of the gathered data for a fixed sampling budget, thus reducing the sample complexity.

Neural DDEs with Learnable Delays for Partially Observed Dynamical Systems

Many successful methods to learn dynamical systems from data have recently been introduced. Such methods often rely on the availability of the system's full state. However, this underlying hypothesis is rather restrictive as it is typically not confirmed in practice, leaving us with partially observed systems. Utilizing the Mori-Zwanzig (MZ) formalism from statistical physics, we demonstrate that Constant Lag Neural Delay Differential Equations (NDDEs) naturally serve as suitable models for partially observed states. In empirical evaluation, we show that such models outperform existing methods on both synthetic and experimental data.

Neural State-Dependent Delay Differential Equations

Discontinuities and delayed terms are encountered in the governing equations of a large class of problems ranging from physics, engineering, medicine to economics. These systems are impossible to be properly modelled and simulated with standard Ordinary Differential Equations (ODE), or any data-driven approximation including Neural Ordinary Differential Equations (NODE). To circumvent this issue, latent variables are typically introduced to solve the dynamics of the system in a higher dimensional space and obtain the solution as a projection to the original space. However, this solution lacks physical interpretability. In contrast, Delay Differential Equations (DDEs) and their data-driven, approximated counterparts naturally appear as good candidates to characterize such complicated systems. In this work we revisit the recently proposed Neural DDE by introducing Neural State-Dependent DDE (SDDDE), a general and flexible framework featuring multiple and state-dependent delays. The developed framework is auto-differentiable and runs efficiently on multiple backends. We show that our method is competitive and outperforms other continuous-class models on a wide variety of delayed dynamical systems.

Continuous Methods : Adaptively intrusive reduced order model closure

Reduced order modeling methods are often used as a mean to reduce simulation costs in industrial applications. Despite their computational advantages, reduced order models (ROMs) often fail to accurately reproduce complex dynamics encountered in real life applications. To address this challenge, we leverage NeuralODEs to propose a novel ROM correction approach based on a time-continuous memory formulation. Finally, experimental results show that our proposed method provides a high level of accuracy while retaining the low computational costs inherent to reduced models.

Continuous Methods : Hamiltonian Domain Translation

This paper proposes a novel approach to domain translation. Leveraging established parallels between generative models and dynamical systems, we propose a reformulation of the Cycle-GAN architecture. By embedding our model with a Hamiltonian structure, we obtain a continuous, expressive and most importantly invertible generative model for domain translation.

CD-ROM: Complementary Deep-Reduced Order Model

Model order reduction through the POD-Galerkin method can lead to dramatic gains in terms of computational efficiency in solving physical problems. However, the applicability of the method to non linear high-dimensional dynamical systems such as the Navier-Stokes equations has been shown to be limited, producing inaccurate and sometimes unstable models. This paper proposes a closure modeling approach for classical POD-Galerkin reduced order models (ROM). We use multi layer perceptrons (MLP) to learn a continuous in time closure model through the recently proposed Neural ODE method. Inspired by Taken's theorem as well as the Mori-Zwanzig formalism, we augment ROMs with a delay differential equation architecture to model non-Markovian effects in reduced models. The proposed model, called CD-ROM (Complementary Deep-Reduced Order Model) is able to retain information from past states of the system and use it to correct the imperfect reduced dynamics. The model can be integrated in time as a system of ordinary differential equations using any classical time marching scheme. We demonstrate the ability of our CD-ROM approach to improve the accuracy of POD-Galerkin models on two CFD examples, even in configurations unseen during training.

Leveraging the structure of dynamical systems for data-driven modeling

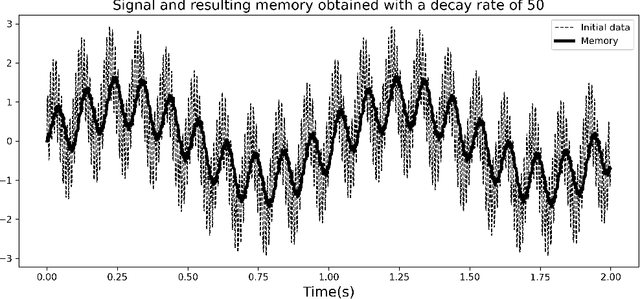
The reliable prediction of the temporal behavior of complex systems is required in numerous scientific fields. This strong interest is however hindered by modeling issues: often, the governing equations describing the physics of the system under consideration are not accessible or, when known, their solution might require a computational time incompatible with the prediction time constraints. Nowadays, approximating complex systems at hand in a generic functional format and informing it ex nihilo from available observations has become a common practice, as illustrated by the enormous amount of scientific work appeared in the last years. Numerous successful examples based on deep neural networks are already available, although generalizability of the models and margins of guarantee are often overlooked. Here, we consider Long-Short Term Memory neural networks and thoroughly investigate the impact of the training set and its structure on the quality of the long-term prediction. Leveraging ergodic theory, we analyze the amount of data sufficient for a priori guaranteeing a faithful model of the physical system. We show how an informed design of the training set, based on invariants of the system and the structure of the underlying attractor, significantly improves the resulting models, opening up avenues for research within the context of active learning. Further, the non-trivial effects of the memory initializations when relying on memory-capable models will be illustrated. Our findings provide evidence-based good-practice on the amount and the choice of data required for an effective data-driven modeling of any complex dynamical system.

Shallow Learning for Fluid Flow Reconstruction with Limited Sensors and Limited Data

In many applications, it is important to reconstruct a fluid flow field, or some other high-dimensional state, from limited measurements and limited data. In this work, we propose a shallow neural network-based learning methodology for such fluid flow reconstruction. Our approach learns an end-to-end mapping between the sensor measurements and the high-dimensional fluid flow field, without any heavy preprocessing on the raw data. No prior knowledge is assumed to be available, and the estimation method is purely data-driven. We demonstrate the performance on three examples in fluid mechanics and oceanography, showing that this modern data-driven approach outperforms traditional modal approximation techniques which are commonly used for flow reconstruction. Not only does the proposed method show superior performance characteristics, it can also produce a comparable level of performance with traditional methods in the area, using significantly fewer sensors. Thus, the mathematical architecture is ideal for emerging global monitoring technologies where measurement data are often limited.

Diffusion Maps meet Nyström

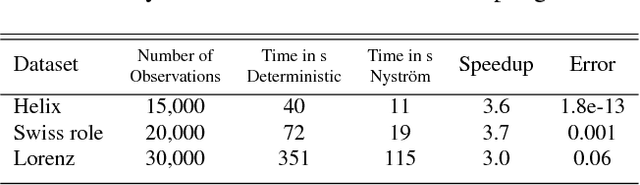
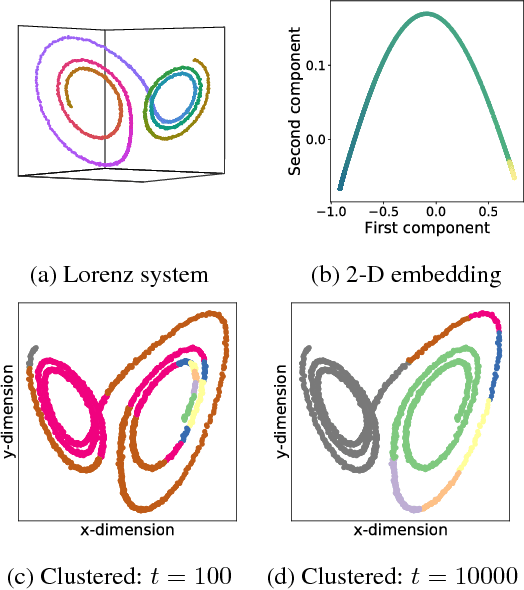
Diffusion maps are an emerging data-driven technique for non-linear dimensionality reduction, which are especially useful for the analysis of coherent structures and nonlinear embeddings of dynamical systems. However, the computational complexity of the diffusion maps algorithm scales with the number of observations. Thus, long time-series data presents a significant challenge for fast and efficient embedding. We propose integrating the Nystr\"om method with diffusion maps in order to ease the computational demand. We achieve a speedup of roughly two to four times when approximating the dominant diffusion map components.