Diffusion Maps meet Nyström
Paper and Code
Feb 23, 2018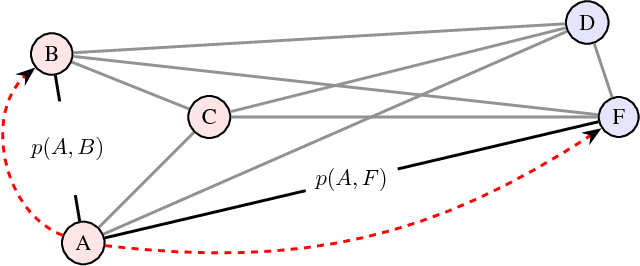
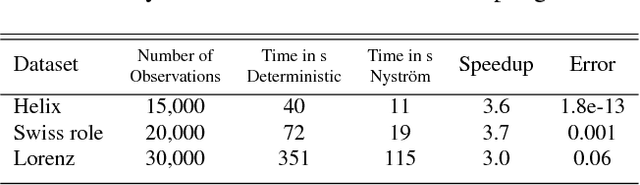

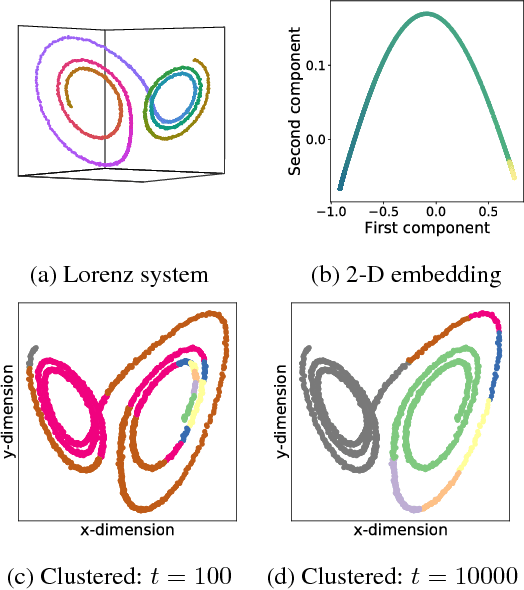
Diffusion maps are an emerging data-driven technique for non-linear dimensionality reduction, which are especially useful for the analysis of coherent structures and nonlinear embeddings of dynamical systems. However, the computational complexity of the diffusion maps algorithm scales with the number of observations. Thus, long time-series data presents a significant challenge for fast and efficient embedding. We propose integrating the Nystr\"om method with diffusion maps in order to ease the computational demand. We achieve a speedup of roughly two to four times when approximating the dominant diffusion map components.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge