Neural DDEs with Learnable Delays for Partially Observed Dynamical Systems

Many successful methods to learn dynamical systems from data have recently been introduced. Such methods often rely on the availability of the system's full state. However, this underlying hypothesis is rather restrictive as it is typically not confirmed in practice, leaving us with partially observed systems. Utilizing the Mori-Zwanzig (MZ) formalism from statistical physics, we demonstrate that Constant Lag Neural Delay Differential Equations (NDDEs) naturally serve as suitable models for partially observed states. In empirical evaluation, we show that such models outperform existing methods on both synthetic and experimental data.

Growing Tiny Networks: Spotting Expressivity Bottlenecks and Fixing Them Optimally

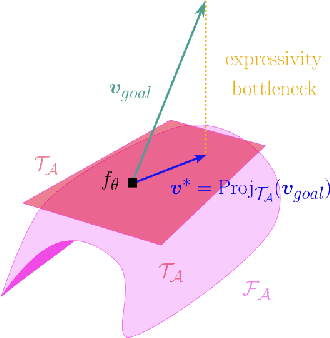
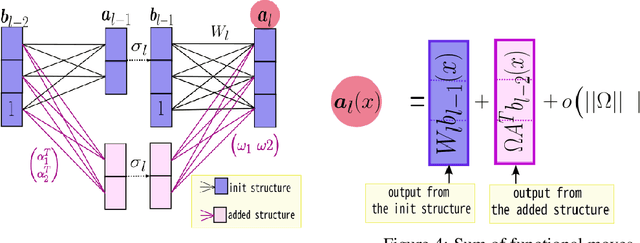
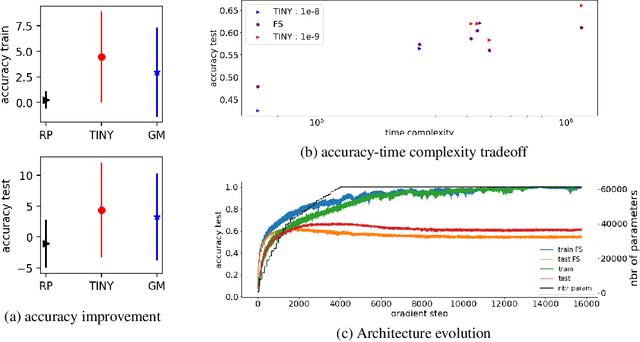
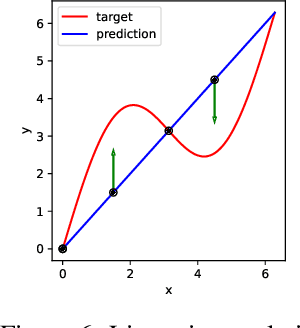
Machine learning tasks are generally formulated as optimization problems, where one searches for an optimal function within a certain functional space. In practice, parameterized functional spaces are considered, in order to be able to perform gradient descent. Typically, a neural network architecture is chosen and fixed, and its parameters (connection weights) are optimized, yielding an architecture-dependent result. This way of proceeding however forces the evolution of the function during training to lie within the realm of what is expressible with the chosen architecture, and prevents any optimization across architectures. Costly architectural hyper-parameter optimization is often performed to compensate for this. Instead, we propose to adapt the architecture on the fly during training. We show that the information about desirable architectural changes, due to expressivity bottlenecks when attempting to follow the functional gradient, can be extracted from %the backpropagation. To do this, we propose a mathematical definition of expressivity bottlenecks, which enables us to detect, quantify and solve them while training, by adding suitable neurons when and where needed. Thus, while the standard approach requires large networks, in terms of number of neurons per layer, for expressivity and optimization reasons, we are able to start with very small neural networks and let them grow appropriately. As a proof of concept, we show results~on the CIFAR dataset, matching large neural network accuracy, with competitive training time, while removing the need for standard architectural hyper-parameter search.

Multi-Level GNN Preconditioner for Solving Large Scale Problems

Large-scale numerical simulations often come at the expense of daunting computations. High-Performance Computing has enhanced the process, but adapting legacy codes to leverage parallel GPU computations remains challenging. Meanwhile, Machine Learning models can harness GPU computations effectively but often struggle with generalization and accuracy. Graph Neural Networks (GNNs), in particular, are great for learning from unstructured data like meshes but are often limited to small-scale problems. Moreover, the capabilities of the trained model usually restrict the accuracy of the data-driven solution. To benefit from both worlds, this paper introduces a novel preconditioner integrating a GNN model within a multi-level Domain Decomposition framework. The proposed GNN-based preconditioner is used to enhance the efficiency of a Krylov method, resulting in a hybrid solver that can converge with any desired level of accuracy. The efficiency of the Krylov method greatly benefits from the GNN preconditioner, which is adaptable to meshes of any size and shape, is executed on GPUs, and features a multi-level approach to enforce the scalability of the entire process. Several experiments are conducted to validate the numerical behavior of the hybrid solver, and an in-depth analysis of its performance is proposed to assess its competitiveness against a C++ legacy solver.

Neural State-Dependent Delay Differential Equations

Discontinuities and delayed terms are encountered in the governing equations of a large class of problems ranging from physics, engineering, medicine to economics. These systems are impossible to be properly modelled and simulated with standard Ordinary Differential Equations (ODE), or any data-driven approximation including Neural Ordinary Differential Equations (NODE). To circumvent this issue, latent variables are typically introduced to solve the dynamics of the system in a higher dimensional space and obtain the solution as a projection to the original space. However, this solution lacks physical interpretability. In contrast, Delay Differential Equations (DDEs) and their data-driven, approximated counterparts naturally appear as good candidates to characterize such complicated systems. In this work we revisit the recently proposed Neural DDE by introducing Neural State-Dependent DDE (SDDDE), a general and flexible framework featuring multiple and state-dependent delays. The developed framework is auto-differentiable and runs efficiently on multiple backends. We show that our method is competitive and outperforms other continuous-class models on a wide variety of delayed dynamical systems.

An Implicit GNN Solver for Poisson-like problems

This paper presents $\Psi$-GNN, a novel Graph Neural Network (GNN) approach for solving the ubiquitous Poisson PDE problems with mixed boundary conditions. By leveraging the Implicit Layer Theory, $\Psi$-GNN models an ''infinitely'' deep network, thus avoiding the empirical tuning of the number of required Message Passing layers to attain the solution. Its original architecture explicitly takes into account the boundary conditions, a critical prerequisite for physical applications, and is able to adapt to any initially provided solution. $\Psi$-GNN is trained using a ''physics-informed'' loss, and the training process is stable by design, and insensitive to its initialization. Furthermore, the consistency of the approach is theoretically proven, and its flexibility and generalization efficiency are experimentally demonstrated: the same learned model can accurately handle unstructured meshes of various sizes, as well as different boundary conditions. To the best of our knowledge, $\Psi$-GNN is the first physics-informed GNN-based method that can handle various unstructured domains, boundary conditions and initial solutions while also providing convergence guarantees.

Designing losses for data-free training of normalizing flows on Boltzmann distributions

Generating a Boltzmann distribution in high dimension has recently been achieved with Normalizing Flows, which enable fast and exact computation of the generated density, and thus unbiased estimation of expectations. However, current implementations rely on accurate training data, which typically comes from computationally expensive simulations. There is therefore a clear incentive to train models with incomplete or no data by relying solely on the target density, which can be obtained from a physical energy model (up to a constant factor). For that purpose, we analyze the properties of standard losses based on Kullback-Leibler divergences. We showcase their limitations, in particular a strong propensity for mode collapse during optimization on high-dimensional distributions. We then propose strategies to alleviate these issues, most importantly a new loss function well-grounded in theory and with suitable optimization properties. Using as a benchmark the generation of 3D molecular configurations, we show on several tasks that, for the first time, imperfect pre-trained models can be further optimized in the absence of training data.

DS-GPS : A Deep Statistical Graph Poisson Solver

This paper proposes a novel Machine Learning-based approach to solve a Poisson problem with mixed boundary conditions. Leveraging Graph Neural Networks, we develop a model able to process unstructured grids with the advantage of enforcing boundary conditions by design. By directly minimizing the residual of the Poisson equation, the model attempts to learn the physics of the problem without the need for exact solutions, in contrast to most previous data-driven processes where the distance with the available solutions is minimized.

SE(3)-equivariant Graph Neural Networks for Learning Glassy Liquids Representations

Within the glassy liquids community, the use of Machine Learning (ML) to model particles' static structure in order to predict their future dynamics is currently a hot topic. The actual state of the art consists in Graph Neural Networks (GNNs) (Bapst 2020) which, beside having a great expressive power, are heavy models with numerous parameters and lack interpretability. Inspired by recent advances (Thomas 2018), we build a GNN that learns a robust representation of the glass' static structure by constraining it to preserve the roto-translation (SE(3)) equivariance. We show that this constraint not only significantly improves the predictive power but also allows to reduce the number of parameters while improving the interpretability. Furthermore, we relate our learned equivariant features to well-known invariant expert features, which are easily expressible with a single layer of our network.

Machine Learning model for gas-liquid interface reconstruction in CFD numerical simulations

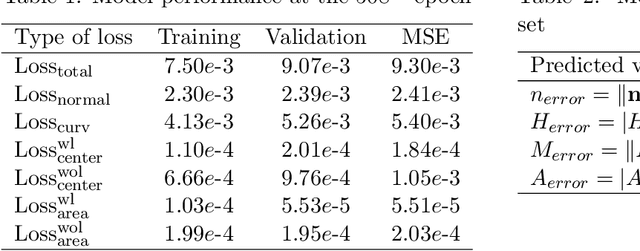
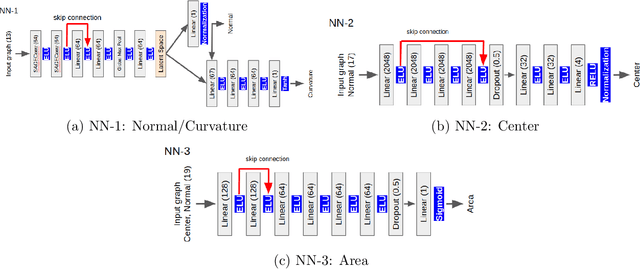
The volume of fluid (VoF) method is widely used in multi-phase flow simulations to track and locate the interface between two immiscible fluids. A major bottleneck of the VoF method is the interface reconstruction step due to its high computational cost and low accuracy on unstructured grids. We propose a machine learning enhanced VoF method based on Graph Neural Networks (GNN) to accelerate the interface reconstruction on general unstructured meshes. We first develop a methodology to generate a synthetic dataset based on paraboloid surfaces discretized on unstructured meshes. We then train a GNN based model and perform generalization tests. Our results demonstrate the efficiency of a GNN based approach for interface reconstruction in multi-phase flow simulations in the industrial context.

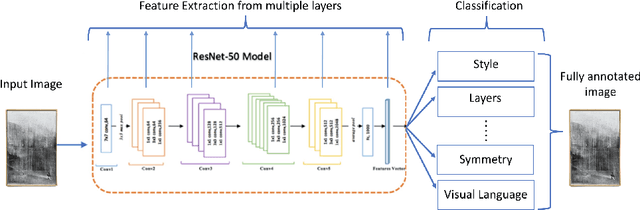
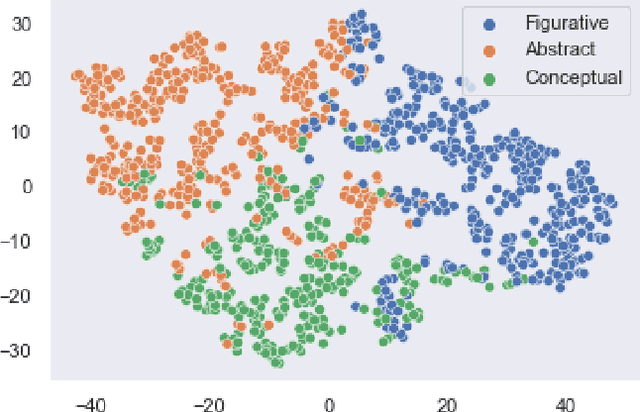
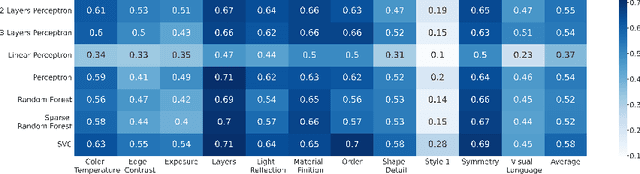
Docent: A content-based recommendation system to discover contemporary art

Recommendation systems have been widely used in various domains such as music, films, e-shopping etc. After mostly avoiding digitization, the art world has recently reached a technological turning point due to the pandemic, making online sales grow significantly as well as providing quantitative online data about artists and artworks. In this work, we present a content-based recommendation system on contemporary art relying on images of artworks and contextual metadata of artists. We gathered and annotated artworks with advanced and art-specific information to create a completely unique database that was used to train our models. With this information, we built a proximity graph between artworks. Similarly, we used NLP techniques to characterize the practices of the artists and we extracted information from exhibitions and other event history to create a proximity graph between artists. The power of graph analysis enables us to provide an artwork recommendation system based on a combination of visual and contextual information from artworks and artists. After an assessment by a team of art specialists, we get an average final rating of 75% of meaningful artworks when compared to their professional evaluations.