SE(3)-equivariant Graph Neural Networks for Learning Glassy Liquids Representations

Within the glassy liquids community, the use of Machine Learning (ML) to model particles' static structure in order to predict their future dynamics is currently a hot topic. The actual state of the art consists in Graph Neural Networks (GNNs) (Bapst 2020) which, beside having a great expressive power, are heavy models with numerous parameters and lack interpretability. Inspired by recent advances (Thomas 2018), we build a GNN that learns a robust representation of the glass' static structure by constraining it to preserve the roto-translation (SE(3)) equivariance. We show that this constraint not only significantly improves the predictive power but also allows to reduce the number of parameters while improving the interpretability. Furthermore, we relate our learned equivariant features to well-known invariant expert features, which are easily expressible with a single layer of our network.

Attractive vs. truncated repulsive supercooled liquids : dynamics is encoded in the pair correlation function

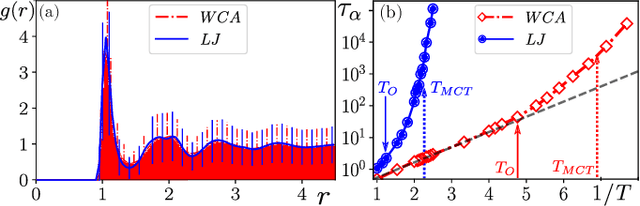
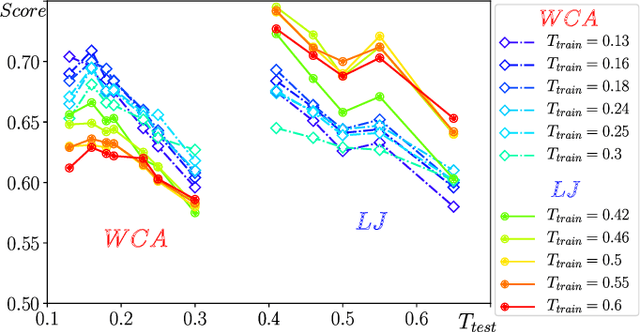
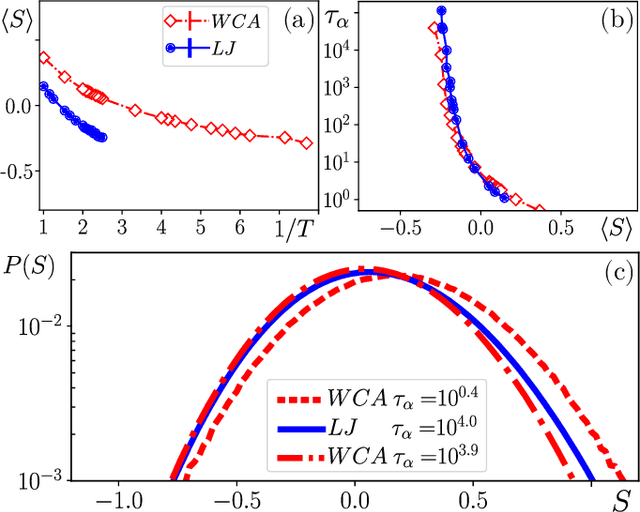
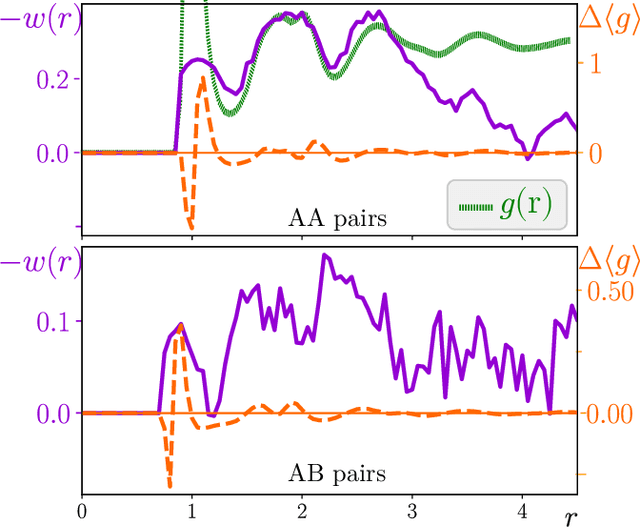
We compare glassy dynamics in two liquids that differ in the form of their interaction potentials. Both systems have the same repulsive interactions but one has also an attractive part in the potential. These two systems exhibit very different dynamics despite having nearly identical pair correlation functions. We demonstrate that a properly weighted integral of the pair correlation function, which amplifies the subtle differences between the two systems, correctly captures their dynamical differences. The weights are obtained from a standard machine learning algorithm.