Designing losses for data-free training of normalizing flows on Boltzmann distributions

Generating a Boltzmann distribution in high dimension has recently been achieved with Normalizing Flows, which enable fast and exact computation of the generated density, and thus unbiased estimation of expectations. However, current implementations rely on accurate training data, which typically comes from computationally expensive simulations. There is therefore a clear incentive to train models with incomplete or no data by relying solely on the target density, which can be obtained from a physical energy model (up to a constant factor). For that purpose, we analyze the properties of standard losses based on Kullback-Leibler divergences. We showcase their limitations, in particular a strong propensity for mode collapse during optimization on high-dimensional distributions. We then propose strategies to alleviate these issues, most importantly a new loss function well-grounded in theory and with suitable optimization properties. Using as a benchmark the generation of 3D molecular configurations, we show on several tasks that, for the first time, imperfect pre-trained models can be further optimized in the absence of training data.

Input Similarity from the Neural Network Perspective

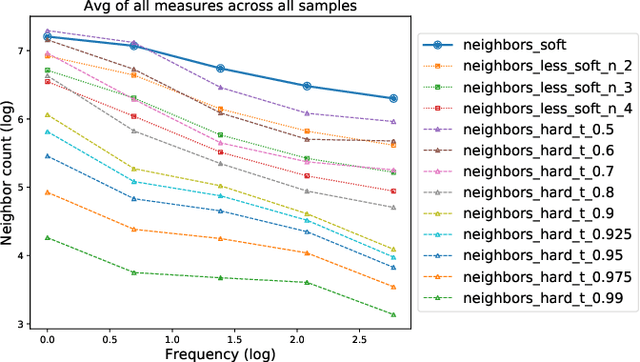
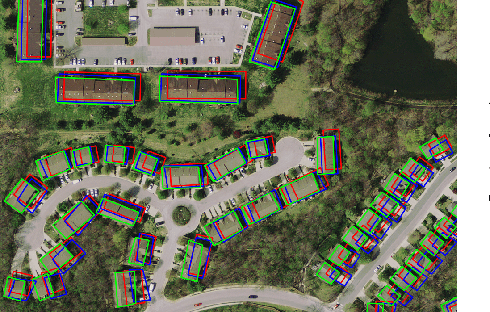
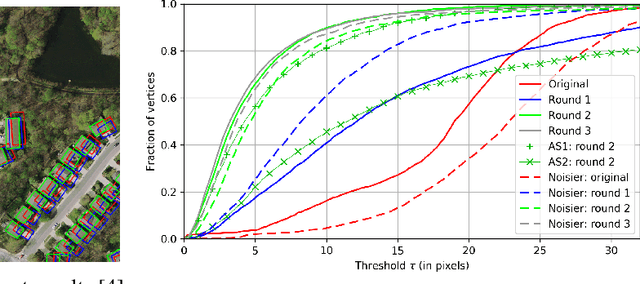
We first exhibit a multimodal image registration task, for which a neural network trained on a dataset with noisy labels reaches almost perfect accuracy, far beyond noise variance. This surprising auto-denoising phenomenon can be explained as a noise averaging effect over the labels of similar input examples. This effect theoretically grows with the number of similar examples; the question is then to define and estimate the similarity of examples. We express a proper definition of similarity, from the neural network perspective, i.e. we quantify how undissociable two inputs $A$ and $B$ are, taking a machine learning viewpoint: how much a parameter variation designed to change the output for $A$ would impact the output for $B$ as well? We study the mathematical properties of this similarity measure, and show how to use it on a trained network to estimate sample density, in low complexity, enabling new types of statistical analysis for neural networks. We analyze data by retrieving samples perceived as similar by the network, and are able to quantify the denoising effect without requiring true labels. We also propose, during training, to enforce that examples known to be similar should also be seen as similar by the network, and notice speed-up training effects for certain datasets.