Input Similarity from the Neural Network Perspective
Paper and Code
Feb 10, 2021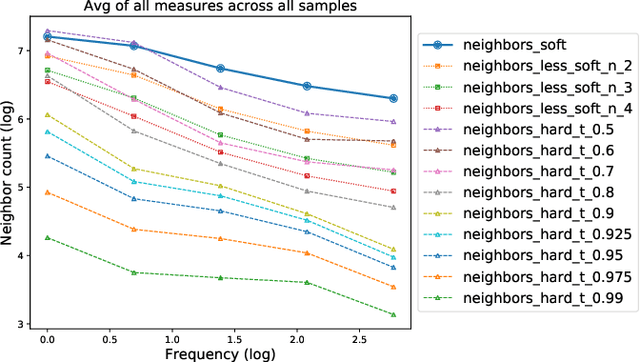
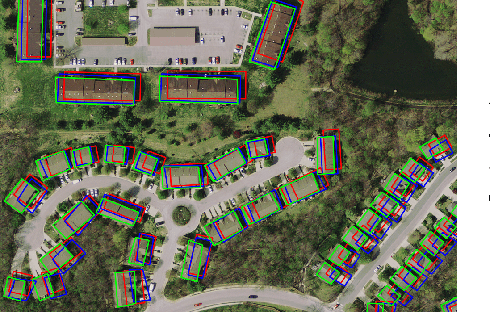
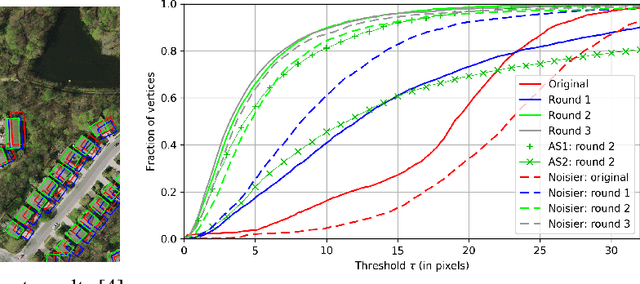

We first exhibit a multimodal image registration task, for which a neural network trained on a dataset with noisy labels reaches almost perfect accuracy, far beyond noise variance. This surprising auto-denoising phenomenon can be explained as a noise averaging effect over the labels of similar input examples. This effect theoretically grows with the number of similar examples; the question is then to define and estimate the similarity of examples. We express a proper definition of similarity, from the neural network perspective, i.e. we quantify how undissociable two inputs $A$ and $B$ are, taking a machine learning viewpoint: how much a parameter variation designed to change the output for $A$ would impact the output for $B$ as well? We study the mathematical properties of this similarity measure, and show how to use it on a trained network to estimate sample density, in low complexity, enabling new types of statistical analysis for neural networks. We analyze data by retrieving samples perceived as similar by the network, and are able to quantify the denoising effect without requiring true labels. We also propose, during training, to enforce that examples known to be similar should also be seen as similar by the network, and notice speed-up training effects for certain datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge