Multi-Level GNN Preconditioner for Solving Large Scale Problems

Large-scale numerical simulations often come at the expense of daunting computations. High-Performance Computing has enhanced the process, but adapting legacy codes to leverage parallel GPU computations remains challenging. Meanwhile, Machine Learning models can harness GPU computations effectively but often struggle with generalization and accuracy. Graph Neural Networks (GNNs), in particular, are great for learning from unstructured data like meshes but are often limited to small-scale problems. Moreover, the capabilities of the trained model usually restrict the accuracy of the data-driven solution. To benefit from both worlds, this paper introduces a novel preconditioner integrating a GNN model within a multi-level Domain Decomposition framework. The proposed GNN-based preconditioner is used to enhance the efficiency of a Krylov method, resulting in a hybrid solver that can converge with any desired level of accuracy. The efficiency of the Krylov method greatly benefits from the GNN preconditioner, which is adaptable to meshes of any size and shape, is executed on GPUs, and features a multi-level approach to enforce the scalability of the entire process. Several experiments are conducted to validate the numerical behavior of the hybrid solver, and an in-depth analysis of its performance is proposed to assess its competitiveness against a C++ legacy solver.

An Implicit GNN Solver for Poisson-like problems

This paper presents $\Psi$-GNN, a novel Graph Neural Network (GNN) approach for solving the ubiquitous Poisson PDE problems with mixed boundary conditions. By leveraging the Implicit Layer Theory, $\Psi$-GNN models an ''infinitely'' deep network, thus avoiding the empirical tuning of the number of required Message Passing layers to attain the solution. Its original architecture explicitly takes into account the boundary conditions, a critical prerequisite for physical applications, and is able to adapt to any initially provided solution. $\Psi$-GNN is trained using a ''physics-informed'' loss, and the training process is stable by design, and insensitive to its initialization. Furthermore, the consistency of the approach is theoretically proven, and its flexibility and generalization efficiency are experimentally demonstrated: the same learned model can accurately handle unstructured meshes of various sizes, as well as different boundary conditions. To the best of our knowledge, $\Psi$-GNN is the first physics-informed GNN-based method that can handle various unstructured domains, boundary conditions and initial solutions while also providing convergence guarantees.

DS-GPS : A Deep Statistical Graph Poisson Solver

This paper proposes a novel Machine Learning-based approach to solve a Poisson problem with mixed boundary conditions. Leveraging Graph Neural Networks, we develop a model able to process unstructured grids with the advantage of enforcing boundary conditions by design. By directly minimizing the residual of the Poisson equation, the model attempts to learn the physics of the problem without the need for exact solutions, in contrast to most previous data-driven processes where the distance with the available solutions is minimized.

HMOE: Hypernetwork-based Mixture of Experts for Domain Generalization

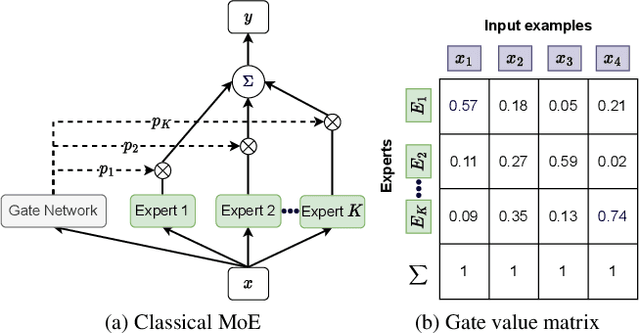
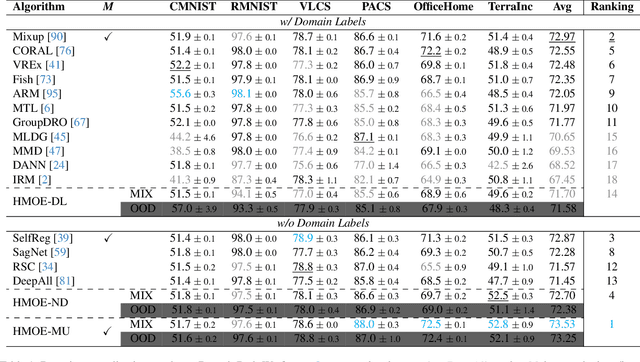
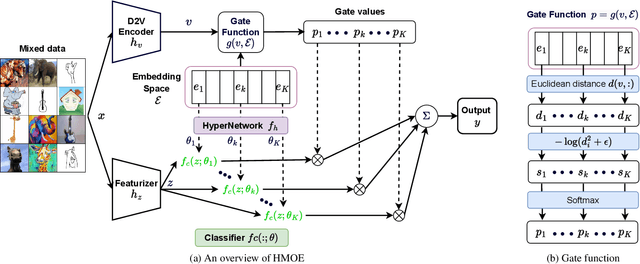
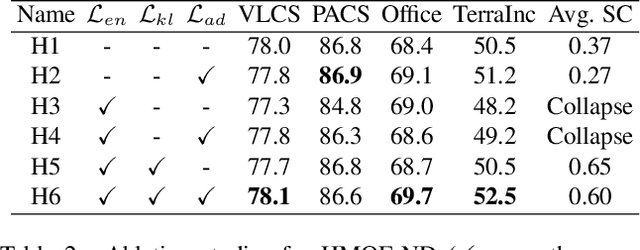
Due to the domain shift, machine learning systems typically fail to generalize well to domains different from those of training data, which is the problem that domain generalization (DG) aims to address. However, most mainstream DG algorithms lack interpretability and require domain labels, which are not available in many real-world scenarios. In this work, we propose a novel DG method, HMOE: Hypernetwork-based Mixture of Experts (MoE), that does not require domain labels and is more interpretable. We use hypernetworks to generate the weights of experts, allowing experts to share some useful meta-knowledge. MoE has proven adept at detecting and identifying heterogeneous patterns in data. For DG, heterogeneity exactly arises from the domain shift. We compare HMOE with other DG algorithms under a fair and unified benchmark-DomainBed. Extensive experiments show that HMOE can perform latent domain discovery from data of mixed domains and divide it into distinct clusters that are surprisingly more consistent with human intuition than original domain labels. Compared to other DG methods, HMOE shows competitive performance and achieves SOTA results in some cases without using domain labels.

Machine Learning model for gas-liquid interface reconstruction in CFD numerical simulations

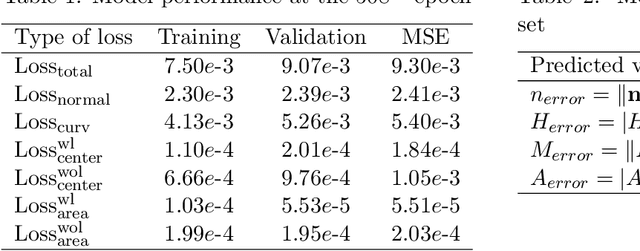
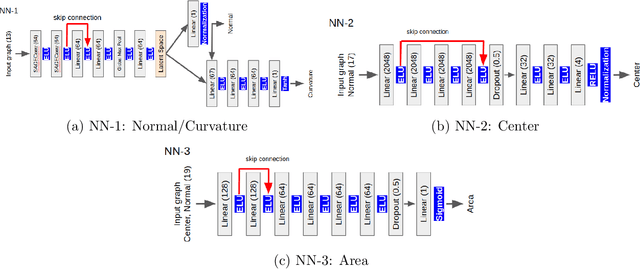
The volume of fluid (VoF) method is widely used in multi-phase flow simulations to track and locate the interface between two immiscible fluids. A major bottleneck of the VoF method is the interface reconstruction step due to its high computational cost and low accuracy on unstructured grids. We propose a machine learning enhanced VoF method based on Graph Neural Networks (GNN) to accelerate the interface reconstruction on general unstructured meshes. We first develop a methodology to generate a synthetic dataset based on paraboloid surfaces discretized on unstructured meshes. We then train a GNN based model and perform generalization tests. Our results demonstrate the efficiency of a GNN based approach for interface reconstruction in multi-phase flow simulations in the industrial context.

PTFlash : A deep learning framework for isothermal two-phase equilibrium calculations

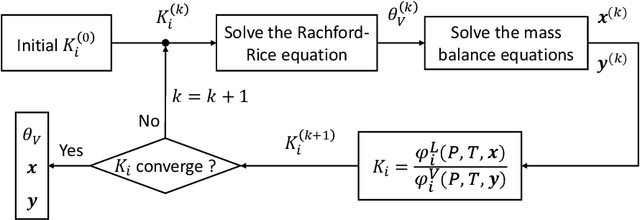
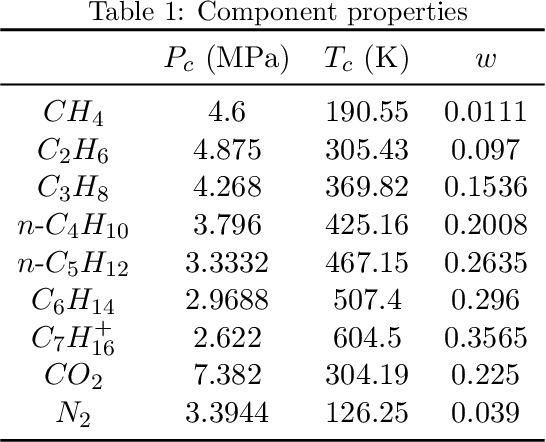
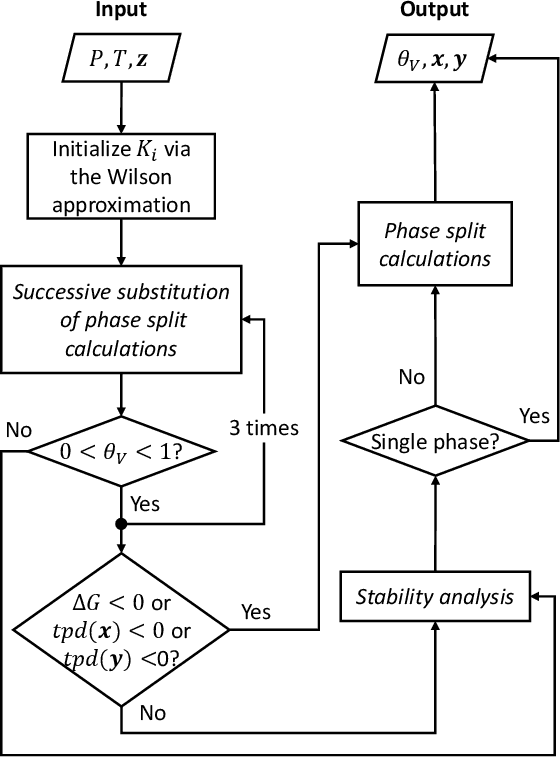
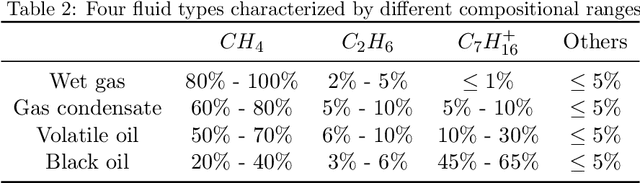
Phase equilibrium calculations are an essential part of numerical simulations of multi-component multi-phase flow in porous media, accounting for the largest share of the computational time. In this work, we introduce a GPUenabled, fast, and parallel framework, PTFlash, that vectorizes algorithms required for isothermal two-phase flash calculations using PyTorch, and can facilitate a wide range of downstream applications. In addition, to further accelerate PTFlash, we design two task-specific neural networks, one for predicting the stability of given mixtures and the other for providing estimates of the distribution coefficients, which are trained offline and help shorten computation time by sidestepping stability analysis and reducing the number of iterations to reach convergence. The evaluation of PTFlash was conducted on three case studies involving hydrocarbons, CO 2 and N 2 , for which the phase equilibrium was tested over a large range of temperature, pressure and composition conditions, using the Soave-Redlich-Kwong (SRK) equation of state. We compare PTFlash with an in-house thermodynamic library, Carnot, written in C++ and performing flash calculations one by one on CPU. Results show speed-ups on large scale calculations up to two order of magnitudes, while maintaining perfect precision with the reference solution provided by Carnot.