BN-SCAFFOLD: controlling the drift of Batch Normalization statistics in Federated Learning

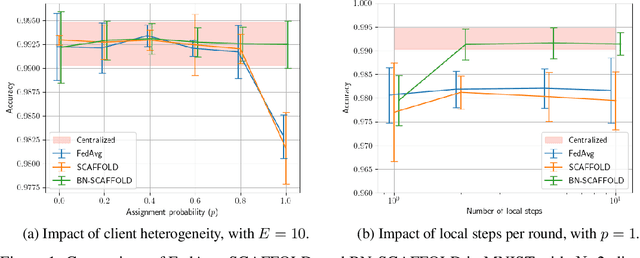
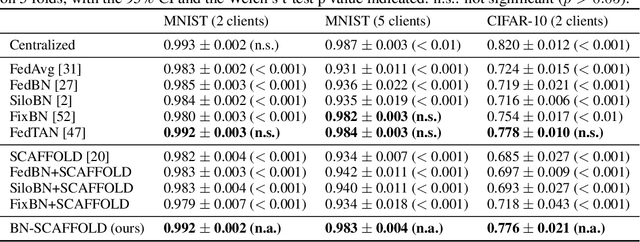
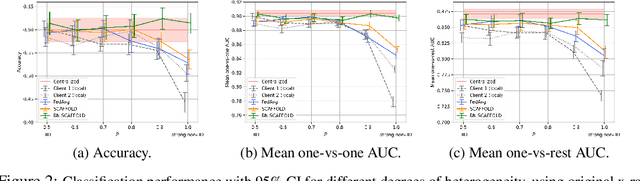
Federated Learning (FL) is gaining traction as a learning paradigm for training Machine Learning (ML) models in a decentralized way. Batch Normalization (BN) is ubiquitous in Deep Neural Networks (DNN), as it improves convergence and generalization. However, BN has been reported to hinder performance of DNNs in heterogeneous FL. Recently, the FedTAN algorithm has been proposed to mitigate the effect of heterogeneity on BN, by aggregating BN statistics and gradients from all the clients. However, it has a high communication cost, that increases linearly with the depth of the DNN. SCAFFOLD is a variance reduction algorithm, that estimates and corrects the client drift in a communication-efficient manner. Despite its promising results in heterogeneous FL settings, it has been reported to underperform for models with BN. In this work, we seek to revive SCAFFOLD, and more generally variance reduction, as an efficient way of training DNN with BN in heterogeneous FL. We introduce a unified theoretical framework for analyzing the convergence of variance reduction algorithms in the BN-DNN setting, inspired of by the work of Wang et al. 2023, and show that SCAFFOLD is unable to remove the bias introduced by BN. We thus propose the BN-SCAFFOLD algorithm, which extends the client drift correction of SCAFFOLD to BN statistics. We prove convergence using the aforementioned framework and validate the theoretical results with experiments on MNIST and CIFAR-10. BN-SCAFFOLD equals the performance of FedTAN, without its high communication cost, outperforming Federated Averaging (FedAvg), SCAFFOLD, and other FL algorithms designed to mitigate BN heterogeneity.