Exact Evaluation of the Accuracy of Diffusion Models for Inverse Problems with Gaussian Data Distributions

Used as priors for Bayesian inverse problems, diffusion models have recently attracted considerable attention in the literature. Their flexibility and high variance enable them to generate multiple solutions for a given task, such as inpainting, super-resolution, and deblurring. However, several unresolved questions remain about how well they perform. In this article, we investigate the accuracy of these models when applied to a Gaussian data distribution for deblurring. Within this constrained context, we are able to precisely analyze the discrepancy between the theoretical resolution of inverse problems and their resolution obtained using diffusion models by computing the exact Wasserstein distance between the distribution of the diffusion model sampler and the ideal distribution of solutions to the inverse problem. Our findings allow for the comparison of different algorithms from the literature.

Depth Separable architecture for Sentinel-5P Super-Resolution

Sentinel-5P (S5P) satellite provides atmospheric measurements for air quality and climate monitoring. While the S5P satellite offers rich spectral resolution, it inherits physical limitations that restricts its spatial resolution. Super-resolution (SR) techniques can overcome these limitations and enhance the spatial resolution of S5P data. In this work, we introduce a novel SR model specifically designed for S5P data that have eight spectral bands with around 500 channels for each band. Our proposed S5-DSCR model relies on Depth Separable Convolution (DSC) architecture to effectively perform spatial SR by exploiting cross-channel correlations. Quantitative evaluation demonstrates that our model outperforms existing methods for the majority of the spectral bands. This work highlights the potential of leveraging DSC architecture to address the challenges of hyperspectral SR. Our model allows for capturing fine details necessary for precise analysis and paves the way for advancements in air quality monitoring as well as remote sensing applications.

SGSST: Scaling Gaussian Splatting StyleTransfer

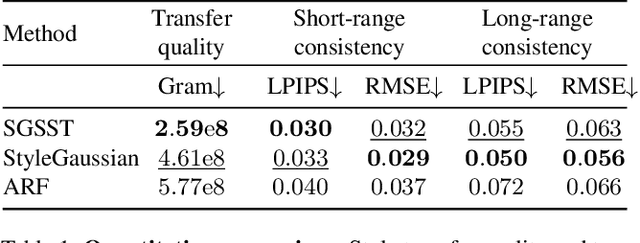
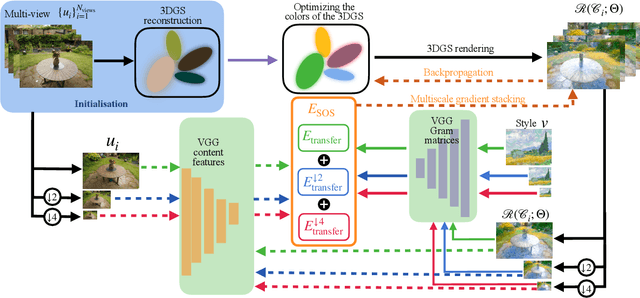
Applying style transfer to a full 3D environment is a challenging task that has seen many developments since the advent of neural rendering. 3D Gaussian splatting (3DGS) has recently pushed further many limits of neural rendering in terms of training speed and reconstruction quality. This work introduces SGSST: Scaling Gaussian Splatting Style Transfer, an optimization-based method to apply style transfer to pretrained 3DGS scenes. We demonstrate that a new multiscale loss based on global neural statistics, that we name SOS for Simultaneously Optimized Scales, enables style transfer to ultra-high resolution 3D scenes. Not only SGSST pioneers 3D scene style transfer at such high image resolutions, it also produces superior visual quality as assessed by thorough qualitative, quantitative and perceptual comparisons.

Adapting MIMO video restoration networks to low latency constraints

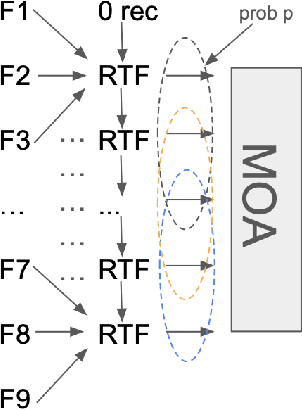
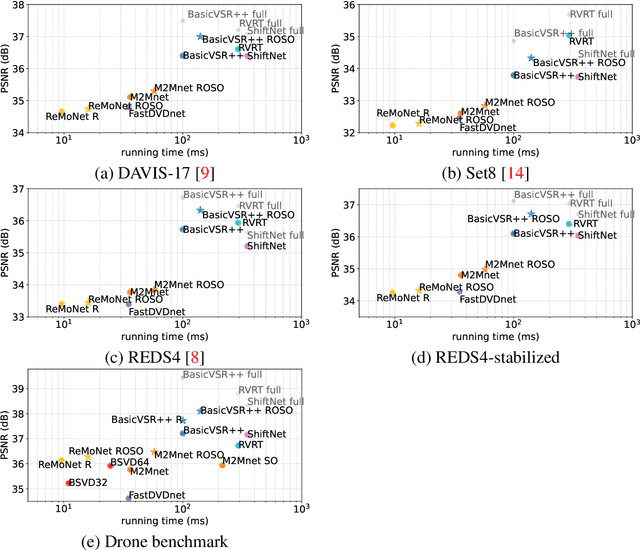
MIMO (multiple input, multiple output) approaches are a recent trend in neural network architectures for video restoration problems, where each network evaluation produces multiple output frames. The video is split into non-overlapping stacks of frames that are processed independently, resulting in a very appealing trade-off between output quality and computational cost. In this work we focus on the low-latency setting by limiting the number of available future frames. We find that MIMO architectures suffer from problems that have received little attention so far, namely (1) the performance drops significantly due to the reduced temporal receptive field, particularly for frames at the borders of the stack, (2) there are strong temporal discontinuities at stack transitions which induce a step-wise motion artifact. We propose two simple solutions to alleviate these problems: recurrence across MIMO stacks to boost the output quality by implicitly increasing the temporal receptive field, and overlapping of the output stacks to smooth the temporal discontinuity at stack transitions. These modifications can be applied to any MIMO architecture. We test them on three state-of-the-art video denoising networks with different computational cost. The proposed contributions result in a new state-of-the-art for low-latency networks, both in terms of reconstruction error and temporal consistency. As an additional contribution, we introduce a new benchmark consisting of drone footage that highlights temporal consistency issues that are not apparent in the standard benchmarks.

Diffusion models for Gaussian distributions: Exact solutions and Wasserstein errors

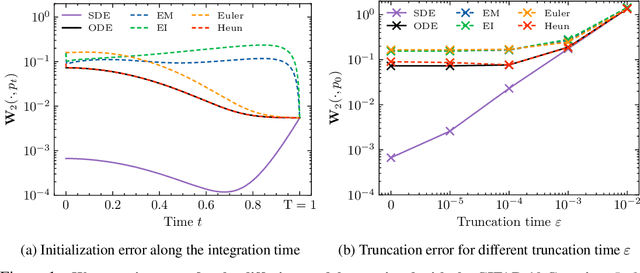
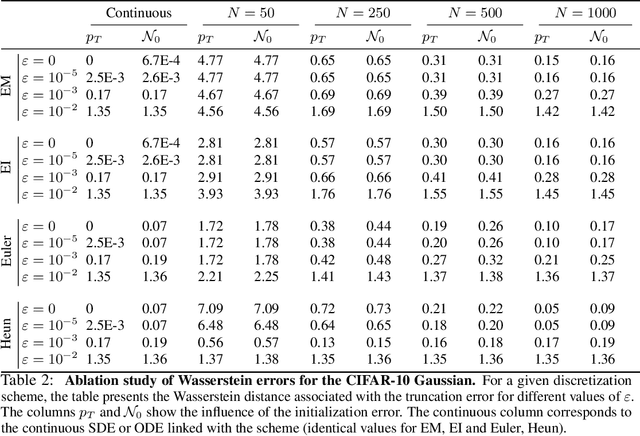
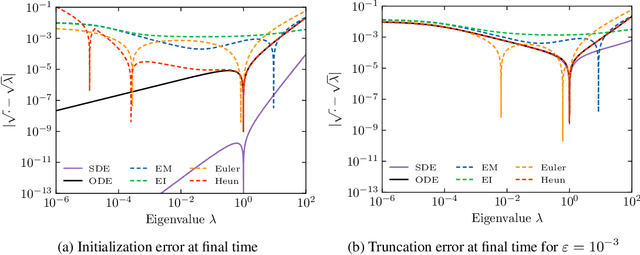
Diffusion or score-based models recently showed high performance in image generation. They rely on a forward and a backward stochastic differential equations (SDE). The sampling of a data distribution is achieved by solving numerically the backward SDE or its associated flow ODE. Studying the convergence of these models necessitates to control four different types of error: the initialization error, the truncation error, the discretization and the score approximation. In this paper, we study theoretically the behavior of diffusion models and their numerical implementation when the data distribution is Gaussian. In this restricted framework where the score function is a linear operator, we can derive the analytical solutions of the forward and backward SDEs as well as the associated flow ODE. This provides exact expressions for various Wasserstein errors which enable us to compare the influence of each error type for any sampling scheme, thus allowing to monitor convergence directly in the data space instead of relying on Inception features. Our experiments show that the recommended numerical schemes from the diffusion models literature are also the best sampling schemes for Gaussian distributions.

Stochastic Super-Resolution For Gaussian Textures

Super-resolution (SR) is an ill-posed inverse problem which consists in proposing high-resolution images consistent with a given low-resolution one. While most SR algorithms are deterministic, stochastic SR deals with designing a stochastic sampler generating any realistic SR solution. The goal of this paper is to show that stochastic SR is a well-posed and solvable problem when restricting to Gaussian stationary textures. Using Gaussian conditional sampling and exploiting the stationarity assumption, we propose an efficient algorithm based on fast Fourier transform. We also demonstrate the practical relevance of the approach for SR with a reference image. Although limited to stationary microtextures, our approach compares favorably in terms of speed and visual quality to some state of the art methods designed for a larger class of images.

On The Role of Alias and Band-Shift for Sentinel-2 Super-Resolution

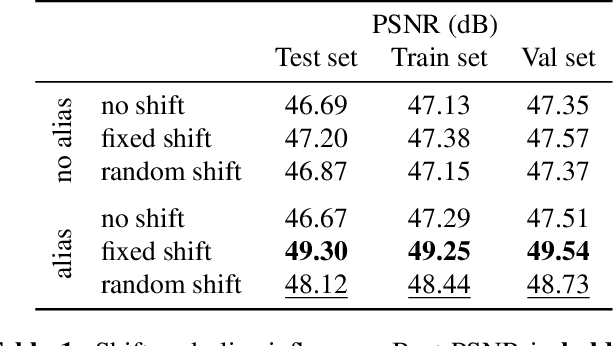
In this work, we study the problem of single-image super-resolution (SISR) of Sentinel-2 imagery. We show that thanks to its unique sensor specification, namely the inter-band shift and alias, that deep-learning methods are able to recover fine details. By training a model using a simple $L_1$ loss, results are free of hallucinated details. For this study, we build a dataset of pairs of images Sentinel-2/PlanetScope to train and evaluate our super-resolution (SR) model.

Scaling Painting Style Transfer

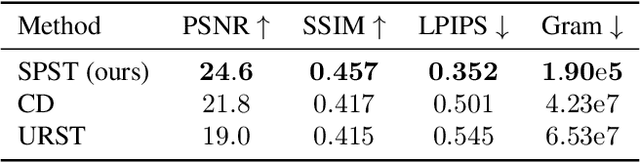
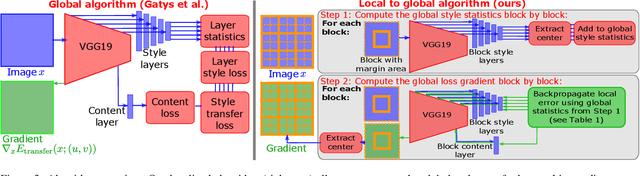
Neural style transfer is a deep learning technique that produces an unprecedentedly rich style transfer from a style image to a content image and is particularly impressive when it comes to transferring style from a painting to an image. It was originally achieved by solving an optimization problem to match the global style statistics of the style image while preserving the local geometric features of the content image. The two main drawbacks of this original approach is that it is computationally expensive and that the resolution of the output images is limited by high GPU memory requirements. Many solutions have been proposed to both accelerate neural style transfer and increase its resolution, but they all compromise the quality of the produced images. Indeed, transferring the style of a painting is a complex task involving features at different scales, from the color palette and compositional style to the fine brushstrokes and texture of the canvas. This paper provides a solution to solve the original global optimization for ultra-high resolution images, enabling multiscale style transfer at unprecedented image sizes. This is achieved by spatially localizing the computation of each forward and backward passes through the VGG network. Extensive qualitative and quantitative comparisons show that our method produces a style transfer of unmatched quality for such high resolution painting styles.

On Demand Solid Texture Synthesis Using Deep 3D Networks

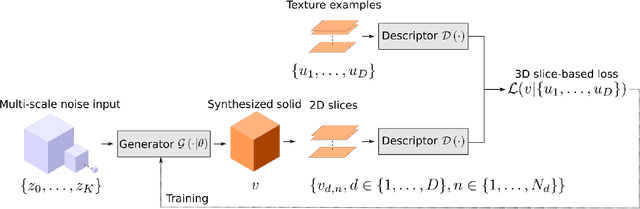
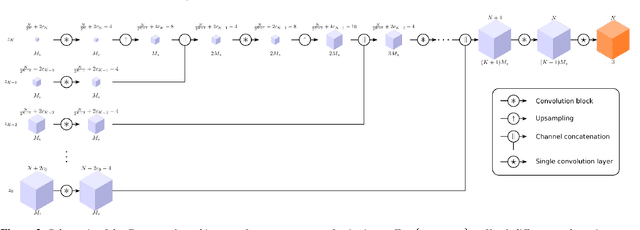
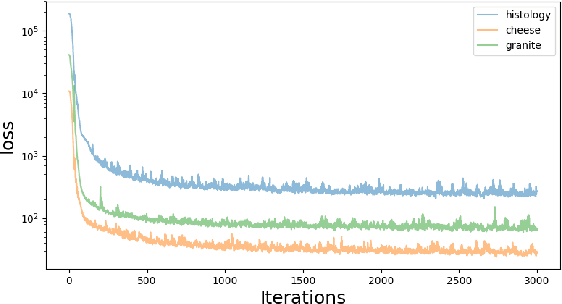
This paper describes a novel approach for on demand volumetric texture synthesis based on a deep learning framework that allows for the generation of high quality 3D data at interactive rates. Based on a few example images of textures, a generative network is trained to synthesize coherent portions of solid textures of arbitrary sizes that reproduce the visual characteristics of the examples along some directions. To cope with memory limitations and computation complexity that are inherent to both high resolution and 3D processing on the GPU, only 2D textures referred to as "slices" are generated during the training stage. These synthetic textures are compared to exemplar images via a perceptual loss function based on a pre-trained deep network. The proposed network is very light (less than 100k parameters), therefore it only requires sustainable training (i.e. few hours) and is capable of very fast generation (around a second for $256^3$ voxels) on a single GPU. Integrated with a spatially seeded PRNG the proposed generator network directly returns an RGB value given a set of 3D coordinates. The synthesized volumes have good visual results that are at least equivalent to the state-of-the-art patch based approaches. They are naturally seamlessly tileable and can be fully generated in parallel.

Maximum entropy methods for texture synthesis: theory and practice

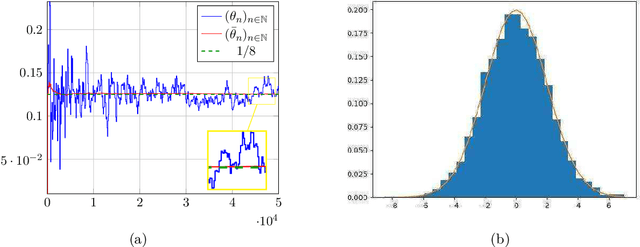
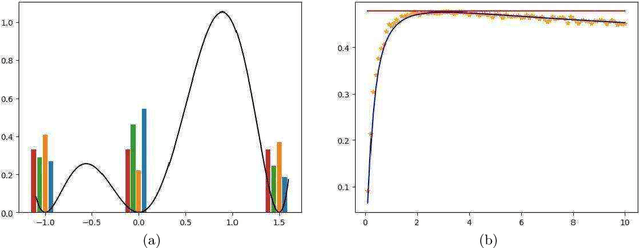
Recent years have seen the rise of convolutional neural network techniques in exemplar-based image synthesis. These methods often rely on the minimization of some variational formulation on the image space for which the minimizers are assumed to be the solutions of the synthesis problem. In this paper we investigate, both theoretically and experimentally, another framework to deal with this problem using an alternate sampling/minimization scheme. First, we use results from information geometry to assess that our method yields a probability measure which has maximum entropy under some constraints in expectation. Then, we turn to the analysis of our method and we show, using recent results from the Markov chain literature, that its error can be explicitly bounded with constants which depend polynomially in the dimension even in the non-convex setting. This includes the case where the constraints are defined via a differentiable neural network. Finally, we present an extensive experimental study of the model, including a comparison with state-of-the-art methods and an extension to style transfer.