Diffusion models for Gaussian distributions: Exact solutions and Wasserstein errors
Paper and Code
May 23, 2024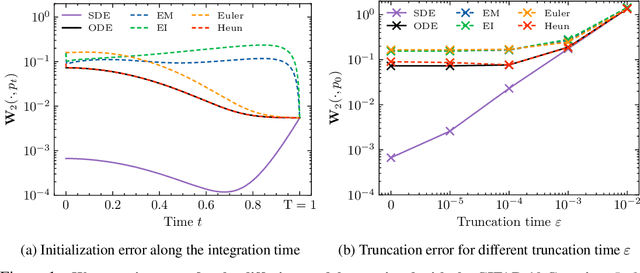

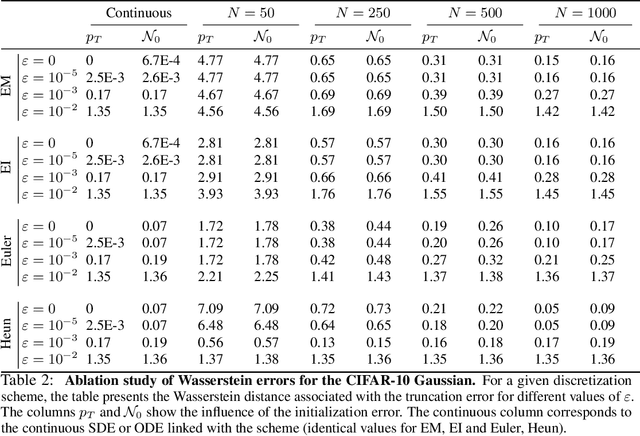
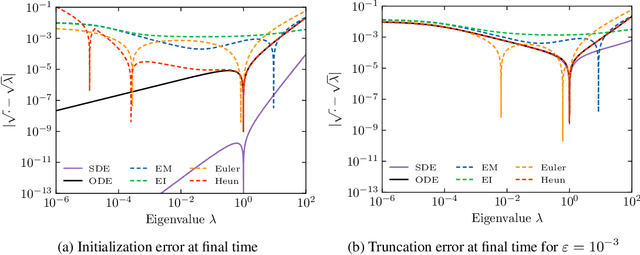
Diffusion or score-based models recently showed high performance in image generation. They rely on a forward and a backward stochastic differential equations (SDE). The sampling of a data distribution is achieved by solving numerically the backward SDE or its associated flow ODE. Studying the convergence of these models necessitates to control four different types of error: the initialization error, the truncation error, the discretization and the score approximation. In this paper, we study theoretically the behavior of diffusion models and their numerical implementation when the data distribution is Gaussian. In this restricted framework where the score function is a linear operator, we can derive the analytical solutions of the forward and backward SDEs as well as the associated flow ODE. This provides exact expressions for various Wasserstein errors which enable us to compare the influence of each error type for any sampling scheme, thus allowing to monitor convergence directly in the data space instead of relying on Inception features. Our experiments show that the recommended numerical schemes from the diffusion models literature are also the best sampling schemes for Gaussian distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge