Exact Evaluation of the Accuracy of Diffusion Models for Inverse Problems with Gaussian Data Distributions

Used as priors for Bayesian inverse problems, diffusion models have recently attracted considerable attention in the literature. Their flexibility and high variance enable them to generate multiple solutions for a given task, such as inpainting, super-resolution, and deblurring. However, several unresolved questions remain about how well they perform. In this article, we investigate the accuracy of these models when applied to a Gaussian data distribution for deblurring. Within this constrained context, we are able to precisely analyze the discrepancy between the theoretical resolution of inverse problems and their resolution obtained using diffusion models by computing the exact Wasserstein distance between the distribution of the diffusion model sampler and the ideal distribution of solutions to the inverse problem. Our findings allow for the comparison of different algorithms from the literature.

Diffusion models for Gaussian distributions: Exact solutions and Wasserstein errors

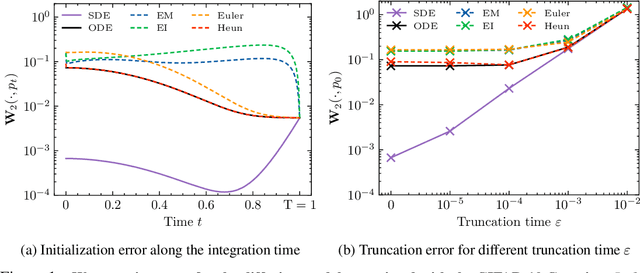
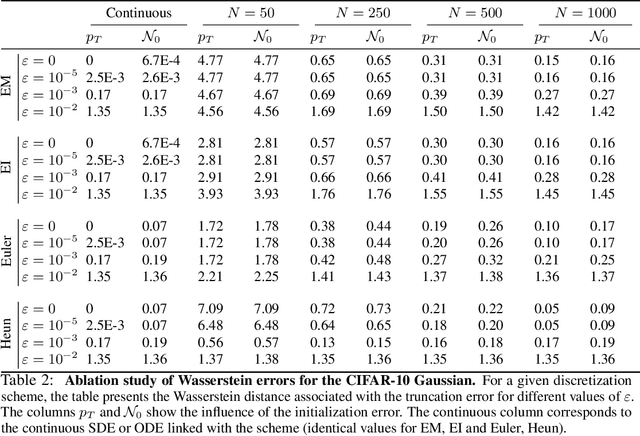
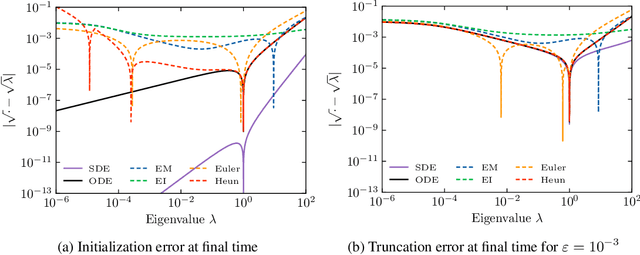
Diffusion or score-based models recently showed high performance in image generation. They rely on a forward and a backward stochastic differential equations (SDE). The sampling of a data distribution is achieved by solving numerically the backward SDE or its associated flow ODE. Studying the convergence of these models necessitates to control four different types of error: the initialization error, the truncation error, the discretization and the score approximation. In this paper, we study theoretically the behavior of diffusion models and their numerical implementation when the data distribution is Gaussian. In this restricted framework where the score function is a linear operator, we can derive the analytical solutions of the forward and backward SDEs as well as the associated flow ODE. This provides exact expressions for various Wasserstein errors which enable us to compare the influence of each error type for any sampling scheme, thus allowing to monitor convergence directly in the data space instead of relying on Inception features. Our experiments show that the recommended numerical schemes from the diffusion models literature are also the best sampling schemes for Gaussian distributions.

Stochastic Super-Resolution For Gaussian Textures

Super-resolution (SR) is an ill-posed inverse problem which consists in proposing high-resolution images consistent with a given low-resolution one. While most SR algorithms are deterministic, stochastic SR deals with designing a stochastic sampler generating any realistic SR solution. The goal of this paper is to show that stochastic SR is a well-posed and solvable problem when restricting to Gaussian stationary textures. Using Gaussian conditional sampling and exploiting the stationarity assumption, we propose an efficient algorithm based on fast Fourier transform. We also demonstrate the practical relevance of the approach for SR with a reference image. Although limited to stationary microtextures, our approach compares favorably in terms of speed and visual quality to some state of the art methods designed for a larger class of images.