Exact Sampling of Determinantal Point Processes without Eigendecomposition
Paper and Code
Oct 31, 2018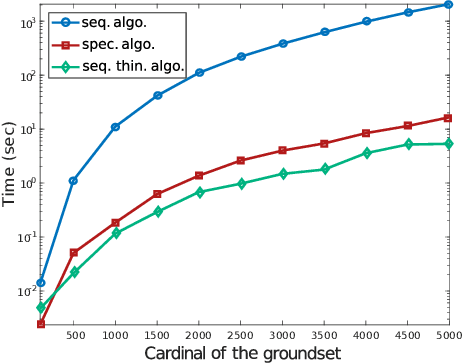
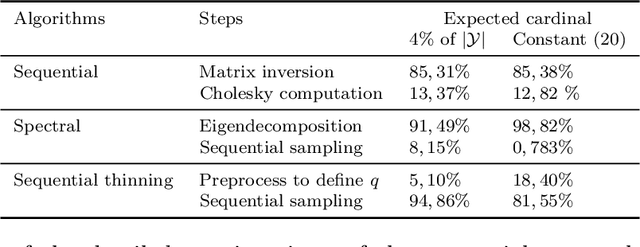
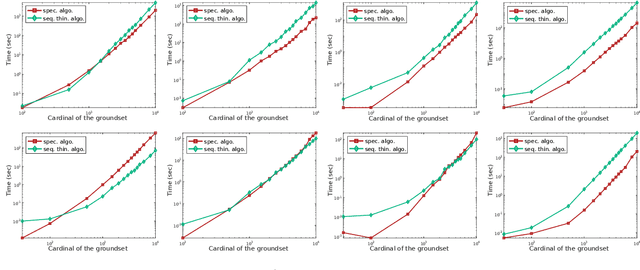
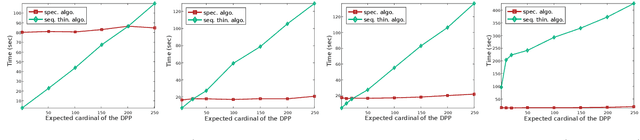
Determinantal point processes (DPPs) enable the modelling of repulsion: they provide diverse sets of points. This repulsion is encoded in a kernel K that we can see as a matrix storing the similarity between points. The usual algorithm to sample DPPs is exact but it uses the spectral decomposition of K, a computation that becomes costly when dealing with a high number of points. Here, we present an alternative exact algorithm that avoids the eigenvalues and the eigenvectors computation and that is, for some applications, faster than the original algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge