Julien Tierny
PEQUAN
Continuous Edit Distance, Geodesics and Barycenters of Time-varying Persistence Diagrams
Dec 15, 2025Abstract:We introduce the Continuous Edit Distance (CED), a geodesic and elastic distance for time-varying persistence diagrams (TVPDs). The CED extends edit-distance ideas to TVPDs by combining local substitution costs with penalized deletions/insertions, controlled by two parameters: \(α\) (trade-off between temporal misalignment and diagram discrepancy) and \(β\) (gap penalty). We also provide an explicit construction of CED-geodesics. Building on these ingredients, we present two practical barycenter solvers, one stochastic and one greedy, that monotonically decrease the CED Frechet energy. Empirically, the CED is robust to additive perturbations (both temporal and spatial), recovers temporal shifts, and supports temporal pattern search. On real-life datasets, the CED achieves clustering performance comparable or better than standard elastic dissimilarities, while our clustering based on CED-barycenters yields superior classification results. Overall, the CED equips TVPD analysis with a principled distance, interpretable geodesics, and practical barycenters, enabling alignment, comparison, averaging, and clustering directly in the space of TVPDs. A C++ implementation is provided for reproducibility at the following address https://github.com/sebastien-tchitchek/ContinuousEditDistance.
Robust Barycenters of Persistence Diagrams
Sep 18, 2025
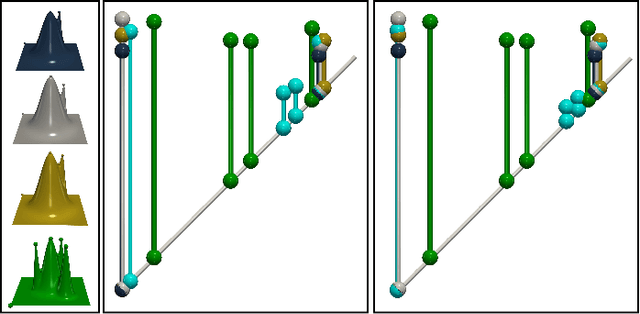
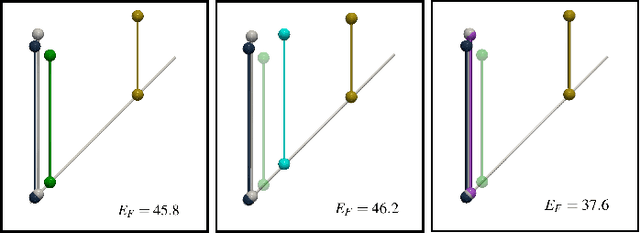
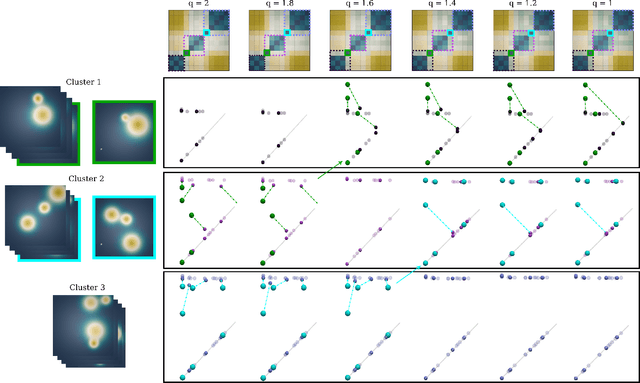
Abstract:This short paper presents a general approach for computing robust Wasserstein barycenters of persistence diagrams. The classical method consists in computing assignment arithmetic means after finding the optimal transport plans between the barycenter and the persistence diagrams. However, this procedure only works for the transportation cost related to the $q$-Wasserstein distance $W_q$ when $q=2$. We adapt an alternative fixed-point method to compute a barycenter diagram for generic transportation costs ($q > 1$), in particular those robust to outliers, $q \in (1,2)$. We show the utility of our work in two applications: \emph{(i)} the clustering of persistence diagrams on their metric space and \emph{(ii)} the dictionary encoding of persistence diagrams. In both scenarios, we demonstrate the added robustness to outliers provided by our generalized framework. Our Python implementation is available at this address: https://github.com/Keanu-Sisouk/RobustBarycenter .
Topology Aware Neural Interpolation of Scalar Fields
Aug 25, 2025Abstract:This paper presents a neural scheme for the topology-aware interpolation of time-varying scalar fields. Given a time-varying sequence of persistence diagrams, along with a sparse temporal sampling of the corresponding scalar fields, denoted as keyframes, our interpolation approach aims at "inverting" the non-keyframe diagrams to produce plausible estimations of the corresponding, missing data. For this, we rely on a neural architecture which learns the relation from a time value to the corresponding scalar field, based on the keyframe examples, and reliably extends this relation to the non-keyframe time steps. We show how augmenting this architecture with specific topological losses exploiting the input diagrams both improves the geometrical and topological reconstruction of the non-keyframe time steps. At query time, given an input time value for which an interpolation is desired, our approach instantaneously produces an output, via a single propagation of the time input through the network. Experiments interpolating 2D and 3D time-varying datasets show our approach superiority, both in terms of data and topological fitting, with regard to reference interpolation schemes.
BondMatcher: H-Bond Stability Analysis in Molecular Systems
Apr 04, 2025Abstract:This application paper investigates the stability of hydrogen bonds (H-bonds), as characterized by the Quantum Theory of Atoms in Molecules (QTAIM). First, we contribute a database of 4544 electron densities associated to four isomers of water hexamers (the so-called Ring, Book, Cage and Prism), generated by distorting their equilibrium geometry under various structural perturbations, modeling the natural dynamic behavior of molecular systems. Second, we present a new stability measure, called bond occurrence rate, associating each bond path present at equilibrium with its rate of occurrence within the input ensemble. We also provide an algorithm, called BondMatcher, for its automatic computation, based on a tailored, geometry-aware partial isomorphism estimation between the extremum graphs of the considered electron densities. Our new stability measure allows for the automatic identification of densities lacking H-bond paths, enabling further visual inspections. Specifically, the topological analysis enabled by our framework corroborates experimental observations and provides refined geometrical criteria for characterizing the disappearance of H-bond paths. Our electron density database and our C++ implementation are available at this address: https://github.com/thom-dani/BondMatcher.
Topological Autoencoders++: Fast and Accurate Cycle-Aware Dimensionality Reduction
Feb 27, 2025Abstract:This paper presents a novel topology-aware dimensionality reduction approach aiming at accurately visualizing the cyclic patterns present in high dimensional data. To that end, we build on the Topological Autoencoders (TopoAE) formulation. First, we provide a novel theoretical analysis of its associated loss and show that a zero loss indeed induces identical persistence pairs (in high and low dimensions) for the $0$-dimensional persistent homology (PH$^0$) of the Rips filtration. We also provide a counter example showing that this property no longer holds for a naive extension of TopoAE to PH$^d$ for $d\ge 1$. Based on this observation, we introduce a novel generalization of TopoAE to $1$-dimensional persistent homology (PH$^1$), called TopoAE++, for the accurate generation of cycle-aware planar embeddings, addressing the above failure case. This generalization is based on the notion of cascade distortion, a new penalty term favoring an isometric embedding of the $2$-chains filling persistent $1$-cycles, hence resulting in more faithful geometrical reconstructions of the $1$-cycles in the plane. We further introduce a novel, fast algorithm for the exact computation of PH for Rips filtrations in the plane, yielding improved runtimes over previously documented topology-aware methods. Our method also achieves a better balance between the topological accuracy, as measured by the Wasserstein distance, and the visual preservation of the cycles in low dimensions. Our C++ implementation is available at https://github.com/MClemot/TopologicalAutoencodersPlusPlus.
A User's Guide to Sampling Strategies for Sliced Optimal Transport
Feb 05, 2025Abstract:This paper serves as a user's guide to sampling strategies for sliced optimal transport. We provide reminders and additional regularity results on the Sliced Wasserstein distance. We detail the construction methods, generation time complexity, theoretical guarantees, and conditions for each strategy. Additionally, we provide insights into their suitability for sliced optimal transport in theory. Extensive experiments on both simulated and real-world data offer a representative comparison of the strategies, culminating in practical recommendations for their best usage.
Identifying Locally Turbulent Vortices within Instabilities
Aug 21, 2024Abstract:This work presents an approach for the automatic detection of locally turbulent vortices within turbulent 2D flows such as instabilites. First, given a time step of the flow, methods from Topological Data Analysis (TDA) are leveraged to extract the geometry of the vortices. Specifically, the enstrophy of the flow is simplified by topological persistence, and the vortices are extracted by collecting the basins of the simplified enstrophy's Morse complex. Next, the local kinetic energy power spectrum is computed for each vortex. We introduce a set of indicators based on the kinetic energy power spectrum to estimate the correlation between the vortex's behavior and that of an idealized turbulent vortex. Our preliminary experiments show the relevance of these indicators for distinguishing vortices which are turbulent from those which have not yet reached a turbulent state and thus known as laminar.
A Practical Solver for Scalar Data Topological Simplification
Jul 17, 2024



Abstract:This paper presents a practical approach for the optimization of topological simplification, a central pre-processing step for the analysis and visualization of scalar data. Given an input scalar field f and a set of "signal" persistence pairs to maintain, our approach produces an output field g that is close to f and which optimizes (i) the cancellation of "non-signal" pairs, while (ii) preserving the "signal" pairs. In contrast to pre-existing simplification algorithms, our approach is not restricted to persistence pairs involving extrema and can thus address a larger class of topological features, in particular saddle pairs in three-dimensional scalar data. Our approach leverages recent generic persistence optimization frameworks and extends them with tailored accelerations specific to the problem of topological simplification. Extensive experiments report substantial accelerations over these frameworks, thereby making topological simplification optimization practical for real-life datasets. Our approach enables a direct visualization and analysis of the topologically simplified data, e.g., via isosurfaces of simplified topology (fewer components and handles). We apply our approach to the extraction of prominent filament structures in three-dimensional data. Specifically, we show that our pre-simplification of the data leads to practical improvements over standard topological techniques for removing filament loops. We also show how our approach can be used to repair genus defects in surface processing. Finally, we provide a C++ implementation for reproducibility purposes.
A Generic Software Framework for Distributed Topological Analysis Pipelines
Oct 12, 2023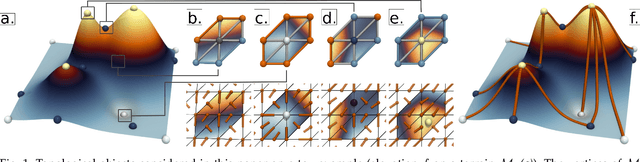
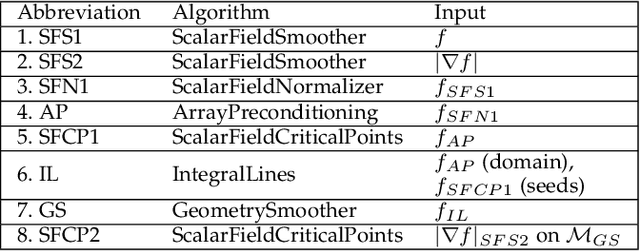
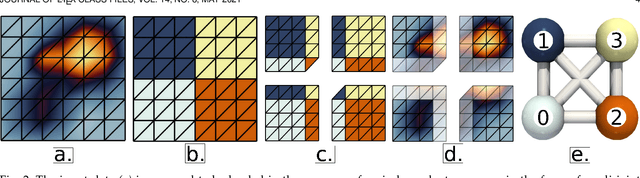
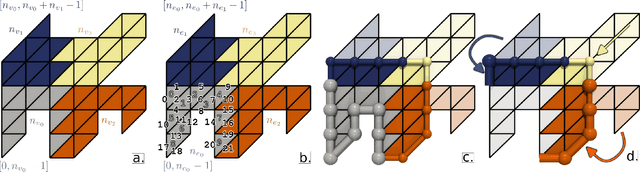
Abstract:This system paper presents a software framework for the support of topological analysis pipelines in a distributed-memory model. While several recent papers introduced topology-based approaches for distributed-memory environments, these were reporting experiments obtained with tailored, mono-algorithm implementations. In contrast, we describe in this paper a general-purpose, generic framework for topological analysis pipelines, i.e. a sequence of topological algorithms interacting together, possibly on distinct numbers of processes. Specifically, we instantiated our framework with the MPI model, within the Topology ToolKit (TTK). While developing this framework, we faced several algorithmic and software engineering challenges, which we document in this paper. We provide a taxonomy for the distributed-memory topological algorithms supported by TTK, depending on their communication needs and provide examples of hybrid MPI+thread parallelizations. Detailed performance analyses show that parallel efficiencies range from $20\%$ to $80\%$ (depending on the algorithms), and that the MPI-specific preconditioning introduced by our framework induces a negligible computation time overhead. We illustrate the new distributed-memory capabilities of TTK with an example of advanced analysis pipeline, combining multiple algorithms, run on the largest publicly available dataset we have found (120 billion vertices) on a standard cluster with 64 nodes (for a total of 1,536 cores). Finally, we provide a roadmap for the completion of TTK's MPI extension, along with generic recommendations for each algorithm communication category.
Wasserstein Auto-Encoders of Merge Trees (and Persistence Diagrams)
Jul 05, 2023Abstract:This paper presents a computational framework for the Wasserstein auto-encoding of merge trees (MT-WAE), a novel extension of the classical auto-encoder neural network architecture to the Wasserstein metric space of merge trees. In contrast to traditional auto-encoders which operate on vectorized data, our formulation explicitly manipulates merge trees on their associated metric space at each layer of the network, resulting in superior accuracy and interpretability. Our novel neural network approach can be interpreted as a non-linear generalization of previous linear attempts [65] at merge tree encoding. It also trivially extends to persistence diagrams. Extensive experiments on public ensembles demonstrate the efficiency of our algorithms, with MT-WAE computations in the orders of minutes on average. We show the utility of our contributions in two applications adapted from previous work on merge tree encoding [65]. First, we apply MT-WAE to data reduction and reliably compress merge trees by concisely representing them with their coordinates in the final layer of our auto-encoder. Second, we document an application to dimensionality reduction, by exploiting the latent space of our auto-encoder, for the visual analysis of ensemble data. We illustrate the versatility of our framework by introducing two penalty terms, to help preserve in the latent space both the Wasserstein distances between merge trees, as well as their clusters. In both applications, quantitative experiments assess the relevance of our framework. Finally, we provide a C++ implementation that can be used for reproducibility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge