BondMatcher: H-Bond Stability Analysis in Molecular Systems

This application paper investigates the stability of hydrogen bonds (H-bonds), as characterized by the Quantum Theory of Atoms in Molecules (QTAIM). First, we contribute a database of 4544 electron densities associated to four isomers of water hexamers (the so-called Ring, Book, Cage and Prism), generated by distorting their equilibrium geometry under various structural perturbations, modeling the natural dynamic behavior of molecular systems. Second, we present a new stability measure, called bond occurrence rate, associating each bond path present at equilibrium with its rate of occurrence within the input ensemble. We also provide an algorithm, called BondMatcher, for its automatic computation, based on a tailored, geometry-aware partial isomorphism estimation between the extremum graphs of the considered electron densities. Our new stability measure allows for the automatic identification of densities lacking H-bond paths, enabling further visual inspections. Specifically, the topological analysis enabled by our framework corroborates experimental observations and provides refined geometrical criteria for characterizing the disappearance of H-bond paths. Our electron density database and our C++ implementation are available at this address: https://github.com/thom-dani/BondMatcher.

Uncertainty quantification for industrial design using dictionaries of reduced order models

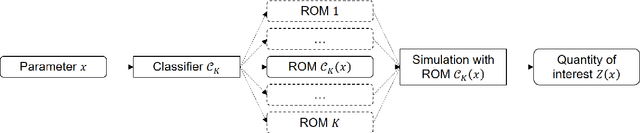
We consider the dictionary-based ROM-net (Reduced Order Model) framework [T. Daniel, F. Casenave, N. Akkari, D. Ryckelynck, Model order reduction assisted by deep neural networks (ROM-net), Advanced modeling and Simulation in Engineering Sciences 7 (16), 2020] and summarize the underlying methodologies and their recent improvements. The main contribution of this work is the application of the complete workflow to a real-life industrial model of an elastoviscoplastic high-pressure turbine blade subjected to thermal, centrifugal and pressure loadings, for the quantification of the uncertainty on dual quantities (such as the accumulated plastic strain and the stress tensor), generated by the uncertainty on the temperature loading field. The dictionary-based ROM-net computes predictions of dual quantities of interest for 1008 Monte Carlo draws of the temperature loading field in 2 hours and 48 minutes, which corresponds to a speedup greater than 600 with respect to a reference parallel solver using domain decomposition, with a relative error in the order of 2%. Another contribution of this work consists in the derivation of a meta-model to reconstruct the dual quantities of interest over the complete mesh from their values on the reduced integration points.

Data augmentation and feature selection for automatic model recommendation in computational physics

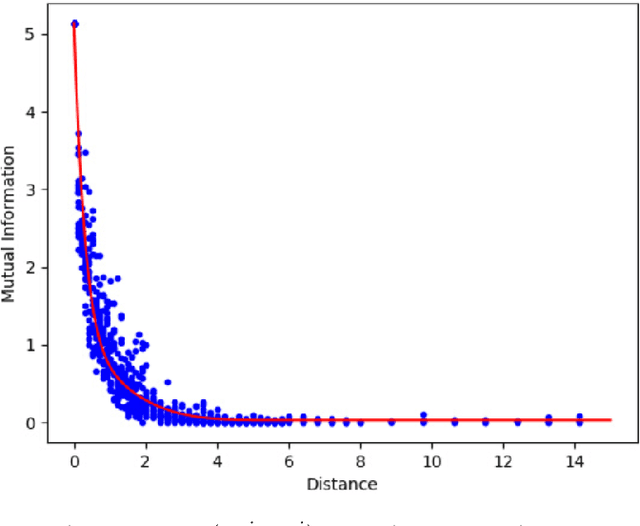
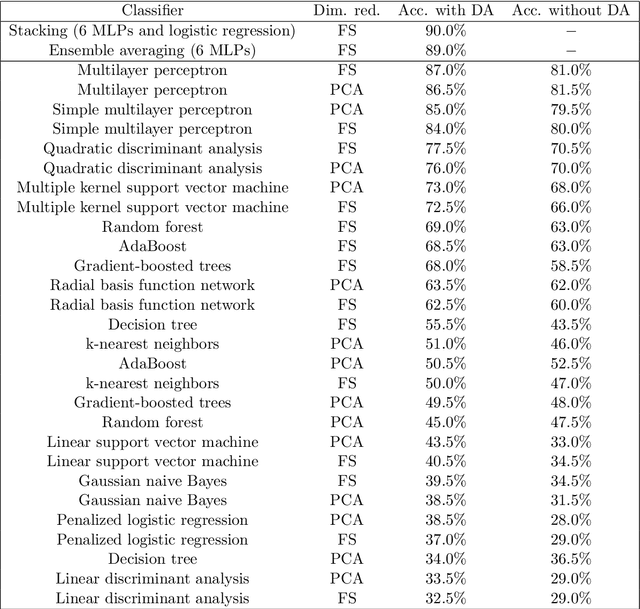
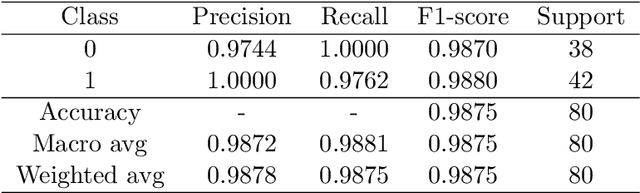
Classification algorithms have recently found applications in computational physics for the selection of numerical methods or models adapted to the environment and the state of the physical system. For such classification tasks, labeled training data come from numerical simulations and generally correspond to physical fields discretized on a mesh. Three challenging difficulties arise: the lack of training data, their high dimensionality, and the non-applicability of common data augmentation techniques to physics data. This article introduces two algorithms to address these issues, one for dimensionality reduction via feature selection, and one for data augmentation. These algorithms are combined with a wide variety of classifiers for their evaluation. When combined with a stacking ensemble made of six multilayer perceptrons and a ridge logistic regression, they enable reaching an accuracy of 90% on our classification problem for nonlinear structural mechanics.