Coupled Laplacian Eigenmaps for Locally-Aware 3D Rigid Point Cloud Matching

Point cloud matching, a crucial technique in computer vision, medical and robotics fields, is primarily concerned with finding correspondences between pairs of point clouds or voxels. In some practical scenarios, emphasizing local differences is crucial for accurately identifying a correct match, thereby enhancing the overall robustness and reliability of the matching process. Commonly used shape descriptors have several limitations and often fail to provide meaningful local insights on the paired geometries. In this work, we propose a new technique, based on graph Laplacian eigenmaps, to match point clouds by taking into account fine local structures. To deal with the order and sign ambiguity of Laplacian eigenmaps, we introduce a new operator, called Coupled Laplacian, that allows to easily generate aligned eigenspaces for multiple rigidly-registered geometries. We show that the similarity between those aligned high-dimensional spaces provides a locally meaningful score to match shapes. We initially evaluate the performance of the proposed technique in a point-wise manner, specifically focusing on the task of object anomaly localization using the MVTec 3D-AD dataset. Additionally, we define a new medical task, called automatic Bone Side Estimation (BSE), which we address through a global similarity score derived from coupled eigenspaces. In order to test it, we propose a benchmark collecting bone surface structures from various public datasets. Our matching technique, based on Coupled Laplacian, outperforms other methods by reaching an impressive accuracy on both tasks. The code to reproduce our experiments is publicly available at https://github.com/matteo-bastico/CoupledLaplacian and in the Supplementary Code.

A Simple and Robust Framework for Cross-Modality Medical Image Segmentation applied to Vision Transformers

When it comes to clinical images, automatic segmentation has a wide variety of applications and a considerable diversity of input domains, such as different types of Magnetic Resonance Images (MRIs) and Computerized Tomography (CT) scans. This heterogeneity is a challenge for cross-modality algorithms that should equally perform independently of the input image type fed to them. Often, segmentation models are trained using a single modality, preventing generalization to other types of input data without resorting to transfer learning techniques. Furthermore, the multi-modal or cross-modality architectures proposed in the literature frequently require registered images, which are not easy to collect in clinical environments, or need additional processing steps, such as synthetic image generation. In this work, we propose a simple framework to achieve fair image segmentation of multiple modalities using a single conditional model that adapts its normalization layers based on the input type, trained with non-registered interleaved mixed data. We show that our framework outperforms other cross-modality segmentation methods, when applied to the same 3D UNet baseline model, on the Multi-Modality Whole Heart Segmentation Challenge. Furthermore, we define the Conditional Vision Transformer (C-ViT) encoder, based on the proposed cross-modality framework, and we show that it brings significant improvements to the resulting segmentation, up to 6.87\% of Dice accuracy, with respect to its baseline reference. The code to reproduce our experiments and the trained model weights are available at https://github.com/matteo-bastico/MI-Seg.

A priori compression of convolutional neural networks for wave simulators

Convolutional neural networks are now seeing widespread use in a variety of fields, including image classification, facial and object recognition, medical imaging analysis, and many more. In addition, there are applications such as physics-informed simulators in which accurate forecasts in real time with a minimal lag are required. The present neural network designs include millions of parameters, which makes it difficult to install such complex models on devices that have limited memory. Compression techniques might be able to resolve these issues by decreasing the size of CNN models that are created by reducing the number of parameters that contribute to the complexity of the models. We propose a compressed tensor format of convolutional layer, a priori, before the training of the neural network. 3-way kernels or 2-way kernels in convolutional layers are replaced by one-way fiters. The overfitting phenomena will be reduced also. The time needed to make predictions or time required for training using the original Convolutional Neural Networks model would be cut significantly if there were fewer parameters to deal with. In this paper we present a method of a priori compressing convolutional neural networks for finite element (FE) predictions of physical data. Afterwards we validate our a priori compressed models on physical data from a FE model solving a 2D wave equation. We show that the proposed convolutinal compression technique achieves equivalent performance as classical convolutional layers with fewer trainable parameters and lower memory footprint.

Uncertainty quantification in a mechanical submodel driven by a Wasserstein-GAN

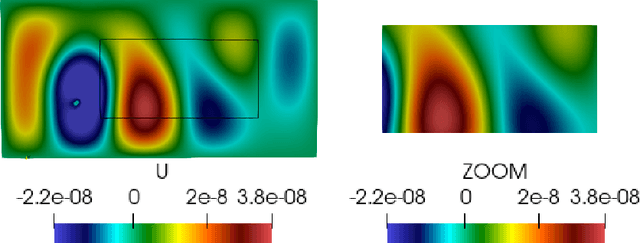
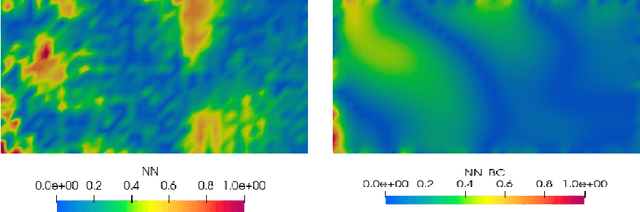
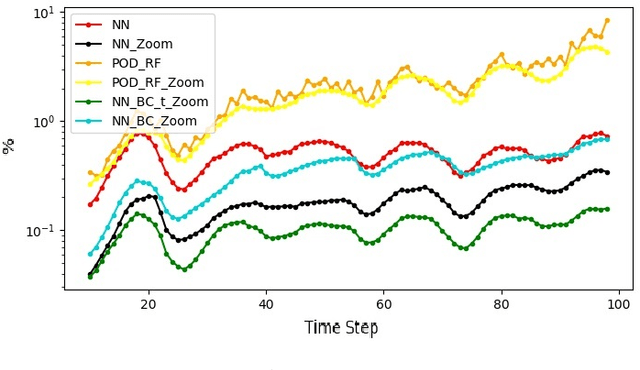
The analysis of parametric and non-parametric uncertainties of very large dynamical systems requires the construction of a stochastic model of said system. Linear approaches relying on random matrix theory and principal componant analysis can be used when systems undergo low-frequency vibrations. In the case of fast dynamics and wave propagation, we investigate a random generator of boundary conditions for fast submodels by using machine learning. We show that the use of non-linear techniques in machine learning and data-driven methods is highly relevant. Physics-informed neural networks is a possible choice for a data-driven method to replace linear modal analysis. An architecture that support a random component is necessary for the construction of the stochastic model of the physical system for non-parametric uncertainties, since the goal is to learn the underlying probabilistic distribution of uncertainty in the data. Generative Adversarial Networks (GANs) are suited for such applications, where the Wasserstein-GAN with gradient penalty variant offers improved convergence results for our problem. The objective of our approach is to train a GAN on data from a finite element method code (Fenics) so as to extract stochastic boundary conditions for faster finite element predictions on a submodel. The submodel and the training data have both the same geometrical support. It is a zone of interest for uncertainty quantification and relevant to engineering purposes. In the exploitation phase, the framework can be viewed as a randomized and parametrized simulation generator on the submodel, which can be used as a Monte Carlo estimator.

Uncertainty quantification for industrial design using dictionaries of reduced order models

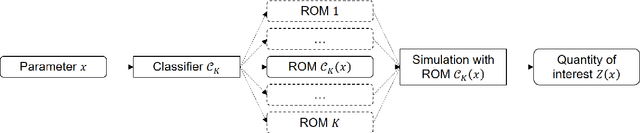
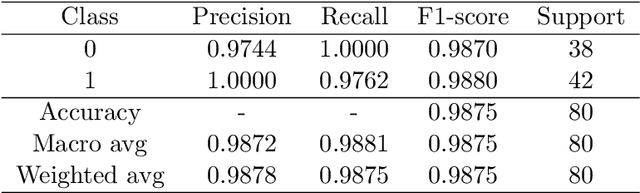
We consider the dictionary-based ROM-net (Reduced Order Model) framework [T. Daniel, F. Casenave, N. Akkari, D. Ryckelynck, Model order reduction assisted by deep neural networks (ROM-net), Advanced modeling and Simulation in Engineering Sciences 7 (16), 2020] and summarize the underlying methodologies and their recent improvements. The main contribution of this work is the application of the complete workflow to a real-life industrial model of an elastoviscoplastic high-pressure turbine blade subjected to thermal, centrifugal and pressure loadings, for the quantification of the uncertainty on dual quantities (such as the accumulated plastic strain and the stress tensor), generated by the uncertainty on the temperature loading field. The dictionary-based ROM-net computes predictions of dual quantities of interest for 1008 Monte Carlo draws of the temperature loading field in 2 hours and 48 minutes, which corresponds to a speedup greater than 600 with respect to a reference parallel solver using domain decomposition, with a relative error in the order of 2%. Another contribution of this work consists in the derivation of a meta-model to reconstruct the dual quantities of interest over the complete mesh from their values on the reduced integration points.

A modular U-Net for automated segmentation of X-ray tomography images in composite materials

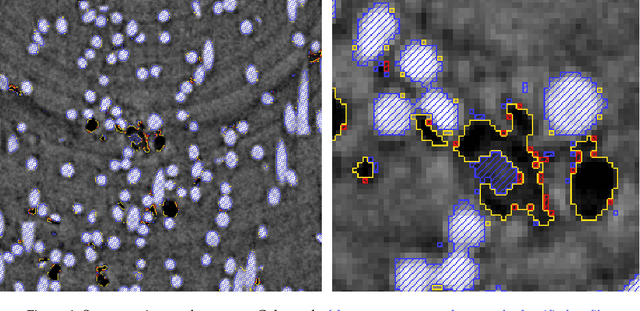
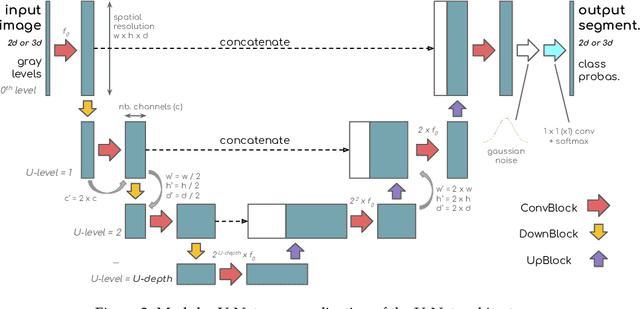
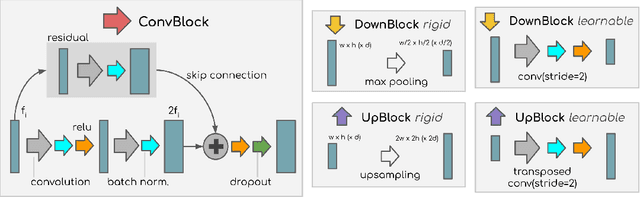
X-ray Computed Tomography (XCT) techniques have evolved to a point that high-resolution data can be acquired so fast that classic segmentation methods are prohibitively cumbersome, demanding automated data pipelines capable of dealing with non-trivial 3D images. Deep learning has demonstrated success in many image processing tasks, including material science applications, showing a promising alternative for a humanfree segmentation pipeline. In this paper a modular interpretation of UNet (Modular U-Net) is proposed and trained to segment 3D tomography images of a three-phased glass fiber-reinforced Polyamide 66. We compare 2D and 3D versions of our model, finding that the former is slightly better than the latter. We observe that human-comparable results can be achievied even with only 10 annotated layers and using a shallow U-Net yields better results than a deeper one. As a consequence, Neural Network (NN) show indeed a promising venue to automate XCT data processing pipelines needing no human, adhoc intervention.

Data augmentation and feature selection for automatic model recommendation in computational physics

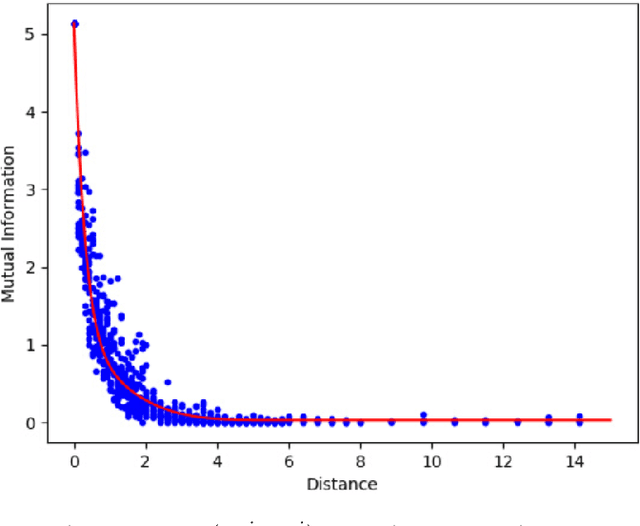
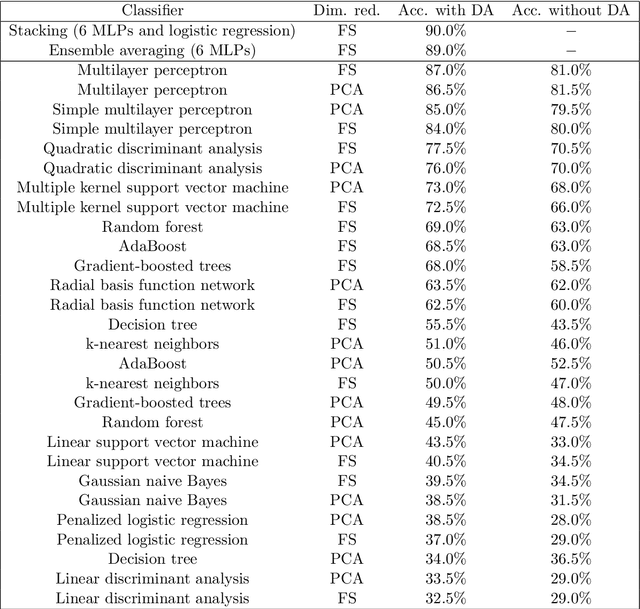
Classification algorithms have recently found applications in computational physics for the selection of numerical methods or models adapted to the environment and the state of the physical system. For such classification tasks, labeled training data come from numerical simulations and generally correspond to physical fields discretized on a mesh. Three challenging difficulties arise: the lack of training data, their high dimensionality, and the non-applicability of common data augmentation techniques to physics data. This article introduces two algorithms to address these issues, one for dimensionality reduction via feature selection, and one for data augmentation. These algorithms are combined with a wide variety of classifiers for their evaluation. When combined with a stacking ensemble made of six multilayer perceptrons and a ridge logistic regression, they enable reaching an accuracy of 90% on our classification problem for nonlinear structural mechanics.

Reduced Bond Graph via machine learning for nonlinear multiphysics dynamic systems

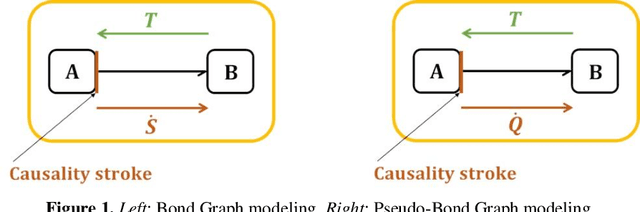
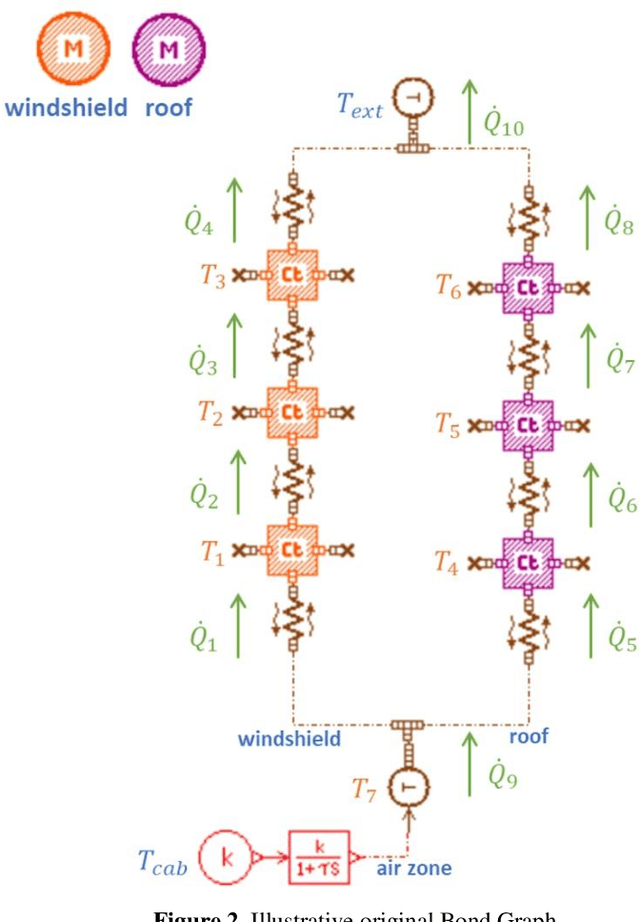
We propose a machine learning approach aiming at reducing Bond Graphs. The output of the machine learning is a hybrid modeling that contains a reduced Bond Graph coupled to a simple artificial neural network. The proposed coupling enables knowledge continuity in machine learning. In this paper, a neural network is obtained by a linear calibration procedure. We propose a method that contains two training steps. First, the method selects the components of the original Bond Graph that are kept in the Reduced Bond Graph. Secondly, the method builds an artificial neural network that supplements the reduced Bond Graph. Because the output of the machine learning is a hybrid model, not solely data, it becomes difficult to use a usual Backpropagation Through Time to calibrate the weights of the neural network. So, in a first attempt, a very simple neural network is proposed by following a model reduction approach. We consider the modeling of the automotive cabins thermal behavior. The data used for the training step are obtained via solutions of differential algebraic equations by using a design of experiment. Simple cooling simulations are run during the training step. We show a simulation speed-up when the reduced bond graph is used to simulate the driving cycle of the WLTP vehicles homologation procedure, while preserving accuracy on output variables. The variables of the original Bond Graph are split into a set of primary variables, a set of secondary variables and a set of tertiary variables. The reduced bond graph contains all the primary variables, but none of the tertiary variables. Secondary variables are coupled to primary ones via an artificial neural network. We discuss the extension of this coupling approach to more complex artificial neural networks.