Pierre Guillou
A Generic Software Framework for Distributed Topological Analysis Pipelines
Oct 12, 2023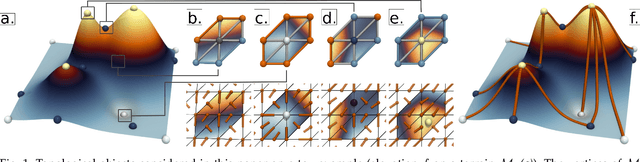
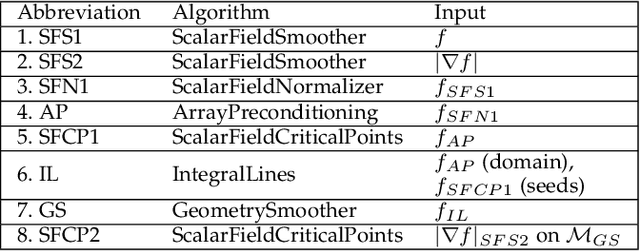
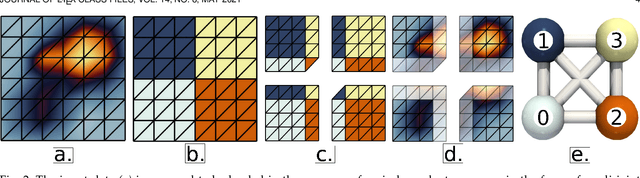
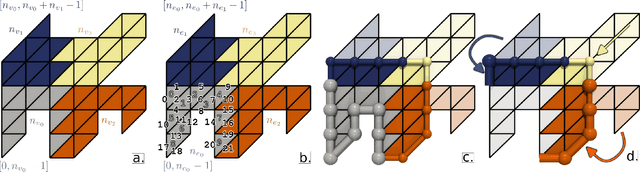
Abstract:This system paper presents a software framework for the support of topological analysis pipelines in a distributed-memory model. While several recent papers introduced topology-based approaches for distributed-memory environments, these were reporting experiments obtained with tailored, mono-algorithm implementations. In contrast, we describe in this paper a general-purpose, generic framework for topological analysis pipelines, i.e. a sequence of topological algorithms interacting together, possibly on distinct numbers of processes. Specifically, we instantiated our framework with the MPI model, within the Topology ToolKit (TTK). While developing this framework, we faced several algorithmic and software engineering challenges, which we document in this paper. We provide a taxonomy for the distributed-memory topological algorithms supported by TTK, depending on their communication needs and provide examples of hybrid MPI+thread parallelizations. Detailed performance analyses show that parallel efficiencies range from $20\%$ to $80\%$ (depending on the algorithms), and that the MPI-specific preconditioning introduced by our framework induces a negligible computation time overhead. We illustrate the new distributed-memory capabilities of TTK with an example of advanced analysis pipeline, combining multiple algorithms, run on the largest publicly available dataset we have found (120 billion vertices) on a standard cluster with 64 nodes (for a total of 1,536 cores). Finally, we provide a roadmap for the completion of TTK's MPI extension, along with generic recommendations for each algorithm communication category.
Discrete Morse Sandwich: Fast Computation of Persistence Diagrams for Scalar Data -- An Algorithm and A Benchmark
Jun 27, 2022
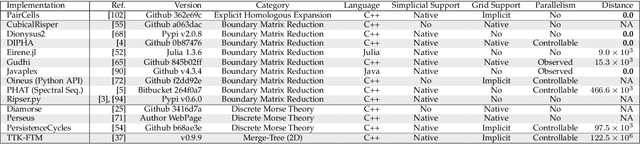
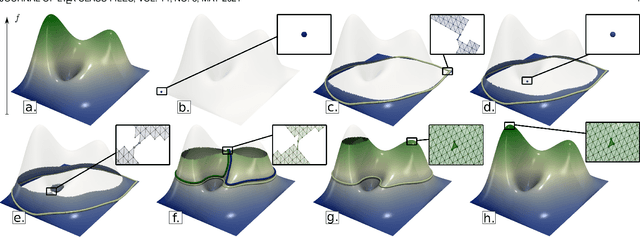
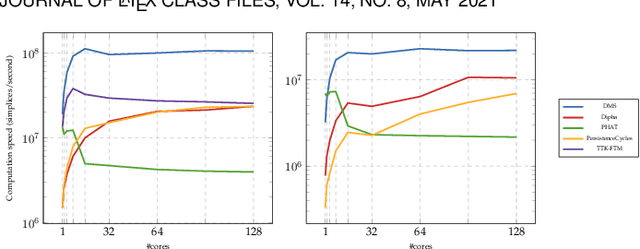
Abstract:This paper introduces an efficient algorithm for persistence diagram computation, given an input piecewise linear scalar field f defined on a d-dimensional simplicial complex K, with $d \leq 3$. Our method extends the seminal "PairCells" algorithm by introducing three main accelerations. First, we express this algorithm within the setting of discrete Morse theory, which considerably reduces the number of input simplices to consider. Second, we introduce a stratification approach to the problem, that we call "sandwiching". Specifically, minima-saddle persistence pairs ($D_0(f)$) and saddle-maximum persistence pairs ($D_{d-1}(f)$) are efficiently computed by respectively processing with a Union-Find the unstable sets of 1-saddles and the stable sets of (d-1)-saddles. This fast processing of the dimensions 0 and (d-1) further reduces, and drastically, the number of critical simplices to consider for the computation of $D_1(f)$, the intermediate layer of the sandwich. Third, we document several performance improvements via shared-memory parallelism. We provide an open-source implementation of our algorithm for reproducibility purposes. We also contribute a reproducible benchmark package, which exploits three-dimensional data from a public repository and compares our algorithm to a variety of publicly available implementations. Extensive experiments indicate that our algorithm improves by two orders of magnitude the time performance of the seminal "PairCells" algorithm it extends. Moreover, it also improves memory footprint and time performance over a selection of 14 competing approaches, with a substantial gain over the fastest available approaches, while producing a strictly identical output. We illustrate the utility of our contributions with an application to the fast and robust extraction of persistent 1-dimensional generators on surfaces, volume data and high-dimensional point clouds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge