Jonas Lukasczyk
TU Kaiserslautern
A Generic Software Framework for Distributed Topological Analysis Pipelines
Oct 12, 2023Abstract:This system paper presents a software framework for the support of topological analysis pipelines in a distributed-memory model. While several recent papers introduced topology-based approaches for distributed-memory environments, these were reporting experiments obtained with tailored, mono-algorithm implementations. In contrast, we describe in this paper a general-purpose, generic framework for topological analysis pipelines, i.e. a sequence of topological algorithms interacting together, possibly on distinct numbers of processes. Specifically, we instantiated our framework with the MPI model, within the Topology ToolKit (TTK). While developing this framework, we faced several algorithmic and software engineering challenges, which we document in this paper. We provide a taxonomy for the distributed-memory topological algorithms supported by TTK, depending on their communication needs and provide examples of hybrid MPI+thread parallelizations. Detailed performance analyses show that parallel efficiencies range from $20\%$ to $80\%$ (depending on the algorithms), and that the MPI-specific preconditioning introduced by our framework induces a negligible computation time overhead. We illustrate the new distributed-memory capabilities of TTK with an example of advanced analysis pipeline, combining multiple algorithms, run on the largest publicly available dataset we have found (120 billion vertices) on a standard cluster with 64 nodes (for a total of 1,536 cores). Finally, we provide a roadmap for the completion of TTK's MPI extension, along with generic recommendations for each algorithm communication category.
Topological Data Analysis Made Easy with the Topology ToolKit
Jun 21, 2018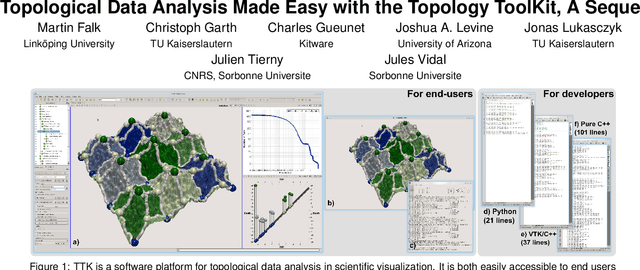
Abstract:This tutorial presents topological methods for the analysis and visualization of scientific data from a user's perspective, with the Topology ToolKit (TTK), a recently released open-source library for topological data analysis. Topological methods have gained considerably in popularity and maturity over the last twenty years and success stories of established methods have been documented in a wide range of applications (combustion, chemistry, astrophysics, material sciences, etc.) with both acquired and simulated data, in both post-hoc and in-situ contexts. While reference textbooks have been published on the topic, no tutorial at IEEE VIS has covered this area in recent years, and never at a software level and from a user's point-of-view. This tutorial fills this gap by providing a beginner's introduction to topological methods for practitioners, researchers, students, and lecturers. In particular, instead of focusing on theoretical aspects and algorithmic details, this tutorial focuses on how topological methods can be useful in practice for concrete data analysis tasks such as segmentation, feature extraction or tracking. The tutorial describes in detail how to achieve these tasks with TTK. First, after an introduction to topological methods and their application in data analysis, a brief overview of TTK's main entry point for end users, namely ParaView, will be presented. Second, an overview of TTK's main features will be given. A running example will be described in detail, showcasing how to access TTK's features via ParaView, Python, VTK/C++, and C++. Third, hands-on sessions will concretely show how to use TTK in ParaView for multiple, representative data analysis tasks. Fourth, the usage of TTK will be presented for developers, in particular by describing several examples of visualization and data analysis projects that were built on top of TTK. Finally, some feedback regarding the usage of TTK as a teaching platform for topological analysis will be given. Presenters of this tutorial include experts in topological methods, core authors of TTK as well as active users, coming from academia, labs, or industry. A large part of the tutorial will be dedicated to hands-on exercises and a rich material package (including TTK pre-installs in virtual machines, code, data, demos, video tutorials, etc.) will be provided to the participants. This tutorial mostly targets students, practitioners and researchers who are not experts in topological methods but who are interested in using them in their daily tasks. We also target researchers already familiar to topological methods and who are interested in using or contributing to TTK.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge