Guillaume Favelier
PEQUAN
Persistence Atlas for Critical Point Variability in Ensembles
Jul 30, 2018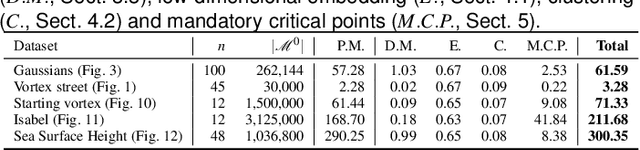



Abstract:This paper presents a new approach for the visualization and analysis of the spatial variability of features of interest represented by critical points in ensemble data. Our framework, called Persistence Atlas, enables the visualization of the dominant spatial patterns of critical points, along with statistics regarding their occurrence in the ensemble. The persistence atlas represents in the geometrical domain each dominant pattern in the form of a confidence map for the appearance of critical points. As a by-product, our method also provides 2-dimensional layouts of the entire ensemble, highlighting the main trends at a global level. Our approach is based on the new notion of Persistence Map, a measure of the geometrical density in critical points which leverages the robustness to noise of topological persistence to better emphasize salient features. We show how to leverage spectral embedding to represent the ensemble members as points in a low-dimensional Euclidean space, where distances between points measure the dissimilarities between critical point layouts and where statistical tasks, such as clustering, can be easily carried out. Further, we show how the notion of mandatory critical point can be leveraged to evaluate for each cluster confidence regions for the appearance of critical points. Most of the steps of this framework can be trivially parallelized and we show how to efficiently implement them. Extensive experiments demonstrate the relevance of our approach. The accuracy of the confidence regions provided by the persistence atlas is quantitatively evaluated and compared to a baseline strategy using an off-the-shelf clustering approach. We illustrate the importance of the persistence atlas in a variety of real-life datasets, where clear trends in feature layouts are identified and analyzed.
Topological Data Analysis Made Easy with the Topology ToolKit
Jun 21, 2018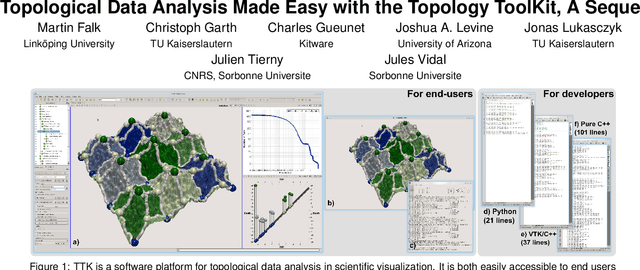
Abstract:This tutorial presents topological methods for the analysis and visualization of scientific data from a user's perspective, with the Topology ToolKit (TTK), a recently released open-source library for topological data analysis. Topological methods have gained considerably in popularity and maturity over the last twenty years and success stories of established methods have been documented in a wide range of applications (combustion, chemistry, astrophysics, material sciences, etc.) with both acquired and simulated data, in both post-hoc and in-situ contexts. While reference textbooks have been published on the topic, no tutorial at IEEE VIS has covered this area in recent years, and never at a software level and from a user's point-of-view. This tutorial fills this gap by providing a beginner's introduction to topological methods for practitioners, researchers, students, and lecturers. In particular, instead of focusing on theoretical aspects and algorithmic details, this tutorial focuses on how topological methods can be useful in practice for concrete data analysis tasks such as segmentation, feature extraction or tracking. The tutorial describes in detail how to achieve these tasks with TTK. First, after an introduction to topological methods and their application in data analysis, a brief overview of TTK's main entry point for end users, namely ParaView, will be presented. Second, an overview of TTK's main features will be given. A running example will be described in detail, showcasing how to access TTK's features via ParaView, Python, VTK/C++, and C++. Third, hands-on sessions will concretely show how to use TTK in ParaView for multiple, representative data analysis tasks. Fourth, the usage of TTK will be presented for developers, in particular by describing several examples of visualization and data analysis projects that were built on top of TTK. Finally, some feedback regarding the usage of TTK as a teaching platform for topological analysis will be given. Presenters of this tutorial include experts in topological methods, core authors of TTK as well as active users, coming from academia, labs, or industry. A large part of the tutorial will be dedicated to hands-on exercises and a rich material package (including TTK pre-installs in virtual machines, code, data, demos, video tutorials, etc.) will be provided to the participants. This tutorial mostly targets students, practitioners and researchers who are not experts in topological methods but who are interested in using them in their daily tasks. We also target researchers already familiar to topological methods and who are interested in using or contributing to TTK.
The Topology ToolKit
May 22, 2018
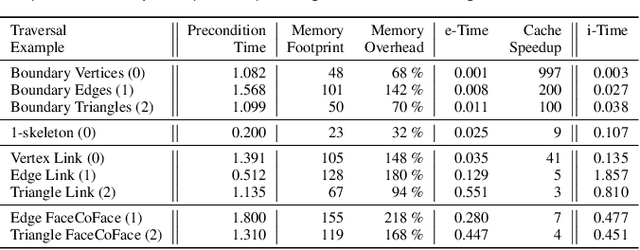
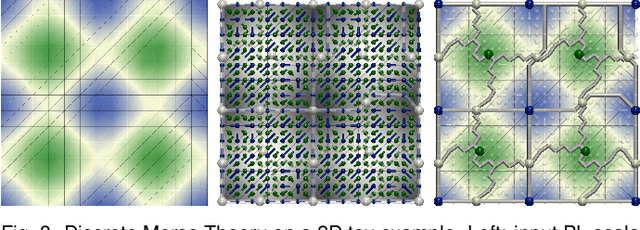

Abstract:This system paper presents the Topology ToolKit (TTK), a software platform designed for topological data analysis in scientific visualization. TTK provides a unified, generic, efficient, and robust implementation of key algorithms for the topological analysis of scalar data, including: critical points, integral lines, persistence diagrams, persistence curves, merge trees, contour trees, Morse-Smale complexes, fiber surfaces, continuous scatterplots, Jacobi sets, Reeb spaces, and more. TTK is easily accessible to end users due to a tight integration with ParaView. It is also easily accessible to developers through a variety of bindings (Python, VTK/C++) for fast prototyping or through direct, dependence-free, C++, to ease integration into pre-existing complex systems. While developing TTK, we faced several algorithmic and software engineering challenges, which we document in this paper. In particular, we present an algorithm for the construction of a discrete gradient that complies to the critical points extracted in the piecewise-linear setting. This algorithm guarantees a combinatorial consistency across the topological abstractions supported by TTK, and importantly, a unified implementation of topological data simplification for multi-scale exploration and analysis. We also present a cached triangulation data structure, that supports time efficient and generic traversals, which self-adjusts its memory usage on demand for input simplicial meshes and which implicitly emulates a triangulation for regular grids with no memory overhead. Finally, we describe an original software architecture, which guarantees memory efficient and direct accesses to TTK features, while still allowing for researchers powerful and easy bindings and extensions. TTK is open source (BSD license) and its code, online documentation and video tutorials are available on TTK's website.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge