Robust supervised classification and feature selection using a primal-dual method

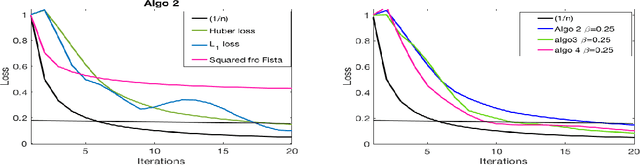
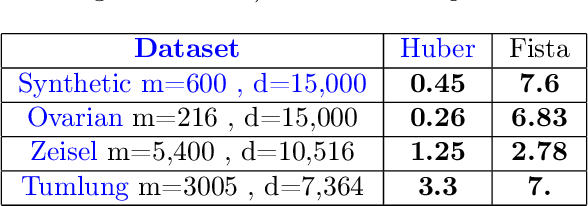
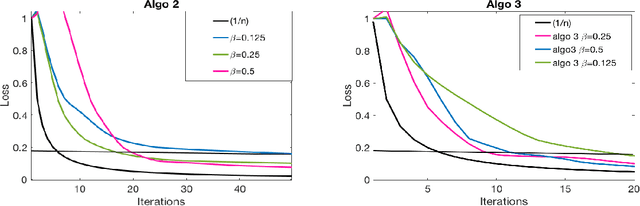
This paper deals with supervised classification and feature selection in high dimensional space. A classical approach is to project data on a low dimensional space and classify by minimizing an appropriate quadratic cost. A strict control on sparsity is moreover obtained by adding an $\ell_1$ constraint, here on the matrix of weights used for projecting the data. Tuning the sparsity bound results in selecting the relevant features for supervised classification. It is well known that using a quadratic cost is not robust to outliers. We cope with this problem by using an $\ell_1$ norm both for the constraint and for the loss function. In this case, the criterion is convex but not gradient Lipschitz anymore. Another second issue is that we optimize simultaneously the projection matrix and the centers used for classification. In this paper, we provide a novel tailored constrained primal-dual method to compute jointly selected features and classifiers. Extending our primal-dual method to other criteria is easy provided that efficient projection (on the dual ball for the loss data term) and prox (for the regularization term) algorithms are available. We illustrate such an extension in the case of a Frobenius norm for the loss term. We provide a convergence proof of our primal-dual method, and demonstrate its effectiveness on three datasets (one synthetic, two from biological data) on which we compare $\ell_1$ and $\ell_2$ costs.

Clustering with feature selection using alternating minimization, Application to computational biology

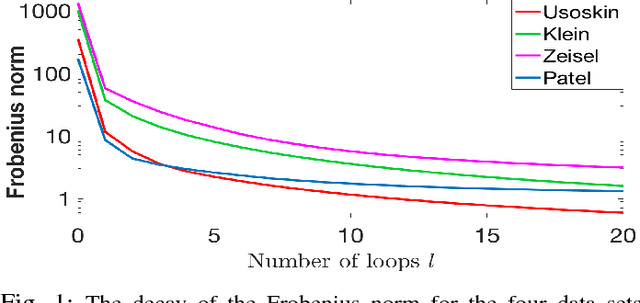
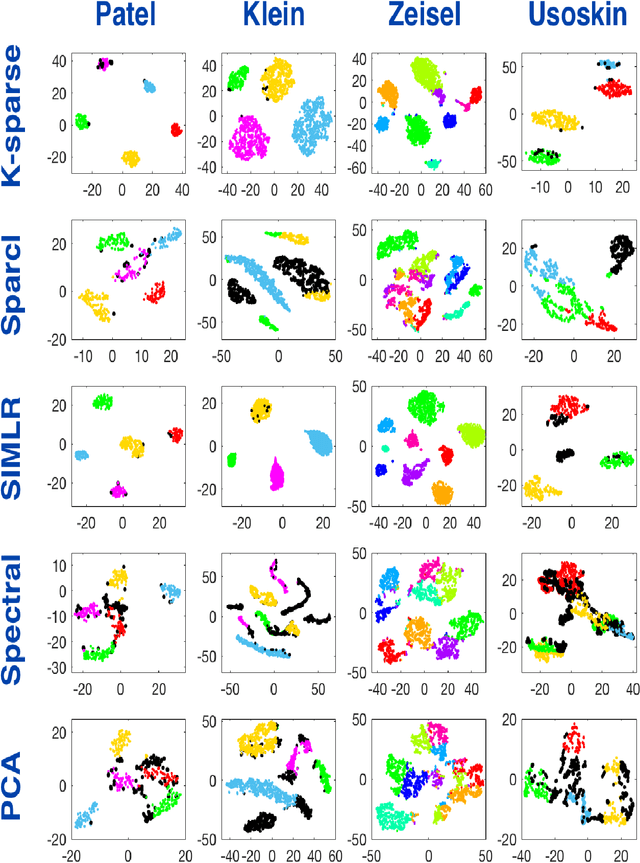
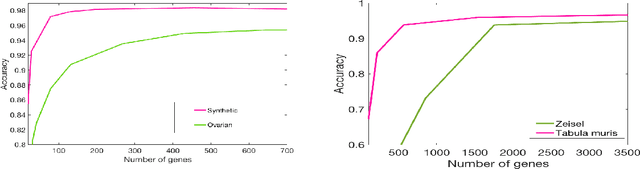
This paper deals with unsupervised clustering with feature selection. The problem is to estimate both labels and a sparse projection matrix of weights. To address this combinatorial non-convex problem maintaining a strict control on the sparsity of the matrix of weights, we propose an alternating minimization of the Frobenius norm criterion. We provide a new efficient algorithm named K-sparse which alternates k-means with projection-gradient minimization. The projection-gradient step is a method of splitting type, with exact projection on the $\ell^1$ ball to promote sparsity. The convergence of the gradient-projection step is addressed, and a preliminary analysis of the alternating minimization is made. The Frobenius norm criterion converges as the number of iterates in Algorithm K-sparse goes to infinity. Experiments on Single Cell RNA sequencing datasets show that our method significantly improves the results of PCA k-means, spectral clustering, SIMLR, and Sparcl methods, and achieves a relevant selection of genes. The complexity of K-sparse is linear in the number of samples (cells), so that the method scales up to large datasets.