Stochastic Primal-Dual Hybrid Gradient Algorithm with Arbitrary Sampling and Imaging Applications
Paper and Code
Apr 10, 2018
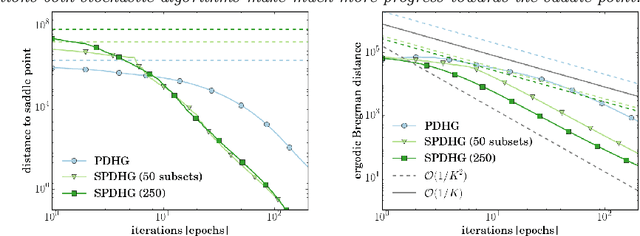
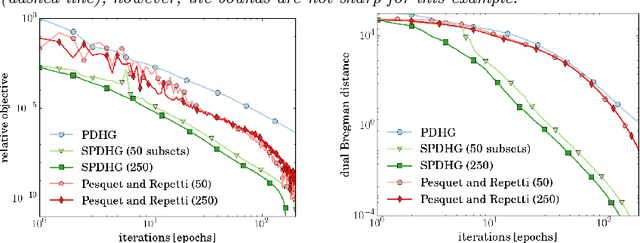

We propose a stochastic extension of the primal-dual hybrid gradient algorithm studied by Chambolle and Pock in 2011 to solve saddle point problems that are separable in the dual variable. The analysis is carried out for general convex-concave saddle point problems and problems that are either partially smooth / strongly convex or fully smooth / strongly convex. We perform the analysis for arbitrary samplings of dual variables, and obtain known deterministic results as a special case. Several variants of our stochastic method significantly outperform the deterministic variant on a variety of imaging tasks.
* 25 pages, 8 figures, submitted
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge