Optimal Transport with Adaptive Regularisation

Regularising the primal formulation of optimal transport (OT) with a strictly convex term leads to enhanced numerical complexity and a denser transport plan. Many formulations impose a global constraint on the transport plan, for instance by relying on entropic regularisation. As it is more expensive to diffuse mass for outlier points compared to central ones, this typically results in a significant imbalance in the way mass is spread across the points. This can be detrimental for some applications where a minimum of smoothing is required per point. To remedy this, we introduce OT with Adaptive RegularIsation (OTARI), a new formulation of OT that imposes constraints on the mass going in or/and out of each point. We then showcase the benefits of this approach for domain adaptation.

Contextual Semantic Interpretability

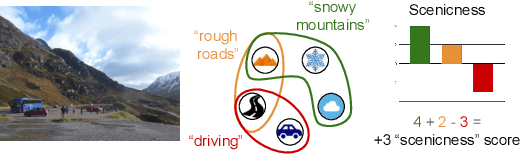
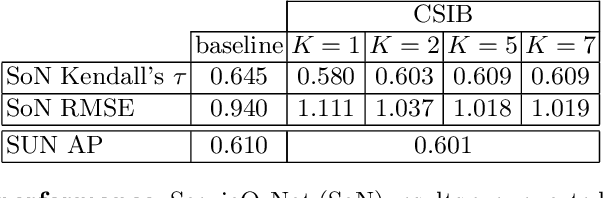
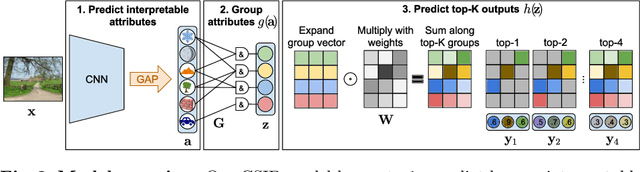
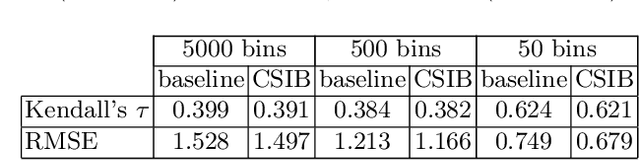
Convolutional neural networks (CNN) are known to learn an image representation that captures concepts relevant to the task, but do so in an implicit way that hampers model interpretability. However, one could argue that such a representation is hidden in the neurons and can be made explicit by teaching the model to recognize semantically interpretable attributes that are present in the scene. We call such an intermediate layer a \emph{semantic bottleneck}. Once the attributes are learned, they can be re-combined to reach the final decision and provide both an accurate prediction and an explicit reasoning behind the CNN decision. In this paper, we look into semantic bottlenecks that capture context: we want attributes to be in groups of a few meaningful elements and participate jointly to the final decision. We use a two-layer semantic bottleneck that gathers attributes into interpretable, sparse groups, allowing them contribute differently to the final output depending on the context. We test our contextual semantic interpretable bottleneck (CSIB) on the task of landscape scenicness estimation and train the semantic interpretable bottleneck using an auxiliary database (SUN Attributes). Our model yields in predictions as accurate as a non-interpretable baseline when applied to a real-world test set of Flickr images, all while providing clear and interpretable explanations for each prediction.

Non-convex regularization in remote sensing

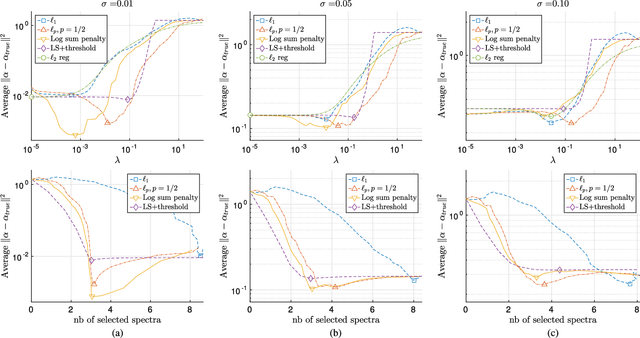
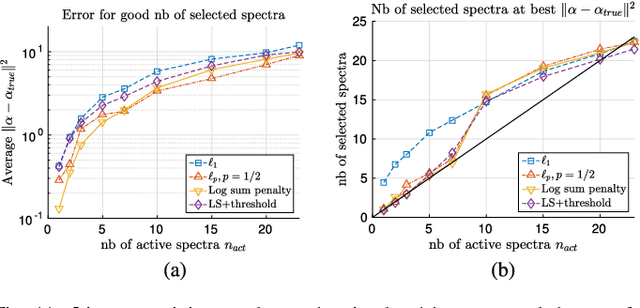
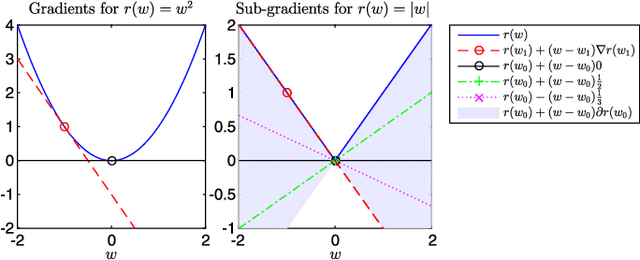
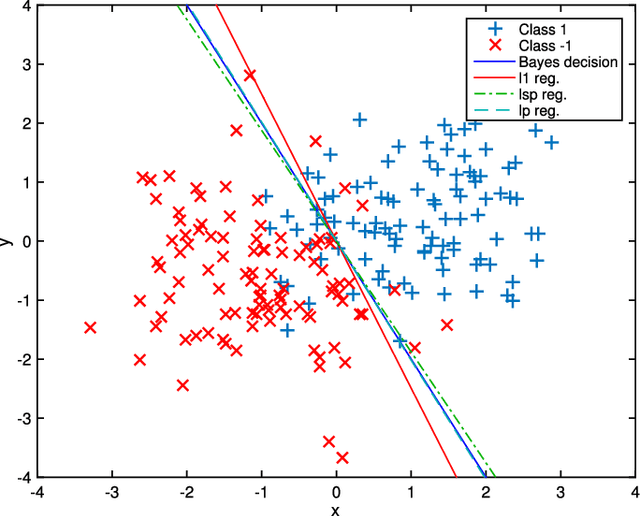
In this paper, we study the effect of different regularizers and their implications in high dimensional image classification and sparse linear unmixing. Although kernelization or sparse methods are globally accepted solutions for processing data in high dimensions, we present here a study on the impact of the form of regularization used and its parametrization. We consider regularization via traditional squared (2) and sparsity-promoting (1) norms, as well as more unconventional nonconvex regularizers (p and Log Sum Penalty). We compare their properties and advantages on several classification and linear unmixing tasks and provide advices on the choice of the best regularizer for the problem at hand. Finally, we also provide a fully functional toolbox for the community.

DC Proximal Newton for Non-Convex Optimization Problems

We introduce a novel algorithm for solving learning problems where both the loss function and the regularizer are non-convex but belong to the class of difference of convex (DC) functions. Our contribution is a new general purpose proximal Newton algorithm that is able to deal with such a situation. The algorithm consists in obtaining a descent direction from an approximation of the loss function and then in performing a line search to ensure sufficient descent. A theoretical analysis is provided showing that the iterates of the proposed algorithm {admit} as limit points stationary points of the DC objective function. Numerical experiments show that our approach is more efficient than current state of the art for a problem with a convex loss functions and non-convex regularizer. We have also illustrated the benefit of our algorithm in high-dimensional transductive learning problem where both loss function and regularizers are non-convex.