Unexpected Improvements to Expected Improvement for Bayesian Optimization
Paper and Code
Oct 31, 2023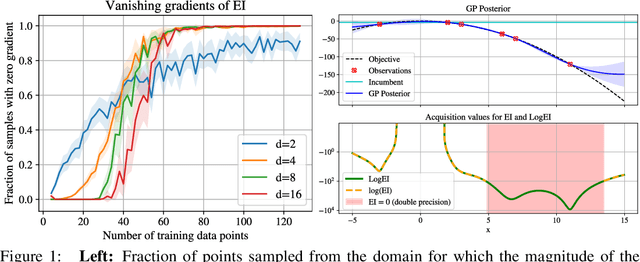

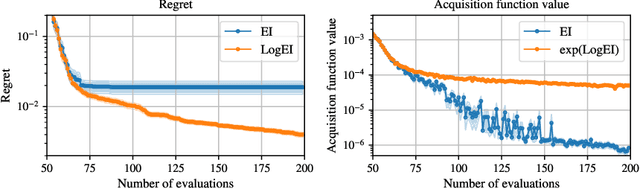
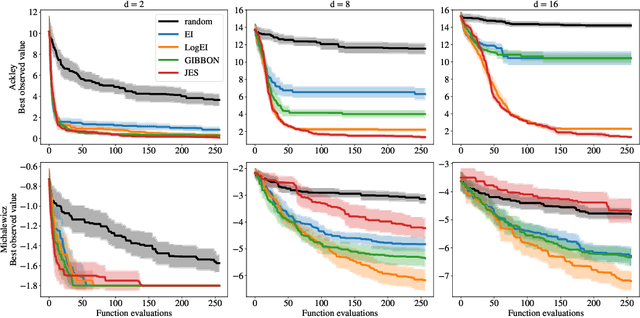
Expected Improvement (EI) is arguably the most popular acquisition function in Bayesian optimization and has found countless successful applications, but its performance is often exceeded by that of more recent methods. Notably, EI and its variants, including for the parallel and multi-objective settings, are challenging to optimize because their acquisition values vanish numerically in many regions. This difficulty generally increases as the number of observations, dimensionality of the search space, or the number of constraints grow, resulting in performance that is inconsistent across the literature and most often sub-optimal. Herein, we propose LogEI, a new family of acquisition functions whose members either have identical or approximately equal optima as their canonical counterparts, but are substantially easier to optimize numerically. We demonstrate that numerical pathologies manifest themselves in "classic" analytic EI, Expected Hypervolume Improvement (EHVI), as well as their constrained, noisy, and parallel variants, and propose corresponding reformulations that remedy these pathologies. Our empirical results show that members of the LogEI family of acquisition functions substantially improve on the optimization performance of their canonical counterparts and surprisingly, are on par with or exceed the performance of recent state-of-the-art acquisition functions, highlighting the understated role of numerical optimization in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge