Sample-Efficient Bayesian Optimization with Transfer Learning for Heterogeneous Search Spaces

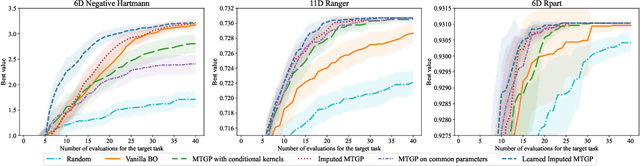
Bayesian optimization (BO) is a powerful approach to sample-efficient optimization of black-box functions. However, in settings with very few function evaluations, a successful application of BO may require transferring information from historical experiments. These related experiments may not have exactly the same tunable parameters (search spaces), motivating the need for BO with transfer learning for heterogeneous search spaces. In this paper, we propose two methods for this setting. The first approach leverages a Gaussian process (GP) model with a conditional kernel to transfer information between different search spaces. Our second approach treats the missing parameters as hyperparameters of the GP model that can be inferred jointly with the other GP hyperparameters or set to fixed values. We show that these two methods perform well on several benchmark problems.

Streamflow Prediction with Uncertainty Quantification for Water Management: A Constrained Reasoning and Learning Approach

Predicting the spatiotemporal variation in streamflow along with uncertainty quantification enables decision-making for sustainable management of scarce water resources. Process-based hydrological models (aka physics-based models) are based on physical laws, but using simplifying assumptions which can lead to poor accuracy. Data-driven approaches offer a powerful alternative, but they require large amount of training data and tend to produce predictions that are inconsistent with physical laws. This paper studies a constrained reasoning and learning (CRL) approach where physical laws represented as logical constraints are integrated as a layer in the deep neural network. To address small data setting, we develop a theoretically-grounded training approach to improve the generalization accuracy of deep models. For uncertainty quantification, we combine the synergistic strengths of Gaussian processes (GPs) and deep temporal models (i.e., deep models for time-series forecasting) by passing the learned latent representation as input to a standard distance-based kernel. Experiments on multiple real-world datasets demonstrate the effectiveness of both CRL and GP with deep kernel approaches over strong baseline methods.

Offline Model-Based Optimization via Policy-Guided Gradient Search

Offline optimization is an emerging problem in many experimental engineering domains including protein, drug or aircraft design, where online experimentation to collect evaluation data is too expensive or dangerous. To avoid that, one has to optimize an unknown function given only its offline evaluation at a fixed set of inputs. A naive solution to this problem is to learn a surrogate model of the unknown function and optimize this surrogate instead. However, such a naive optimizer is prone to erroneous overestimation of the surrogate (possibly due to over-fitting on a biased sample of function evaluation) on inputs outside the offline dataset. Prior approaches addressing this challenge have primarily focused on learning robust surrogate models. However, their search strategies are derived from the surrogate model rather than the actual offline data. To fill this important gap, we introduce a new learning-to-search perspective for offline optimization by reformulating it as an offline reinforcement learning problem. Our proposed policy-guided gradient search approach explicitly learns the best policy for a given surrogate model created from the offline data. Our empirical results on multiple benchmarks demonstrate that the learned optimization policy can be combined with existing offline surrogates to significantly improve the optimization performance.

Bayesian Optimization over High-Dimensional Combinatorial Spaces via Dictionary-based Embeddings

We consider the problem of optimizing expensive black-box functions over high-dimensional combinatorial spaces which arises in many science, engineering, and ML applications. We use Bayesian Optimization (BO) and propose a novel surrogate modeling approach for efficiently handling a large number of binary and categorical parameters. The key idea is to select a number of discrete structures from the input space (the dictionary) and use them to define an ordinal embedding for high-dimensional combinatorial structures. This allows us to use existing Gaussian process models for continuous spaces. We develop a principled approach based on binary wavelets to construct dictionaries for binary spaces, and propose a randomized construction method that generalizes to categorical spaces. We provide theoretical justification to support the effectiveness of the dictionary-based embeddings. Our experiments on diverse real-world benchmarks demonstrate the effectiveness of our proposed surrogate modeling approach over state-of-the-art BO methods.

Uncertainty-Aware Search Framework for Multi-Objective Bayesian Optimization

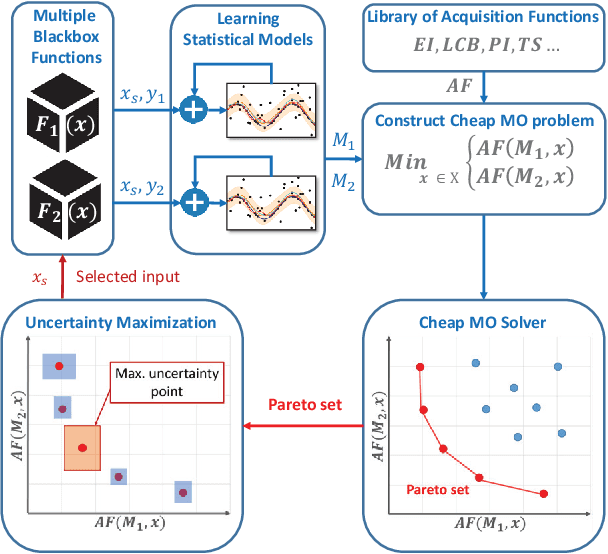
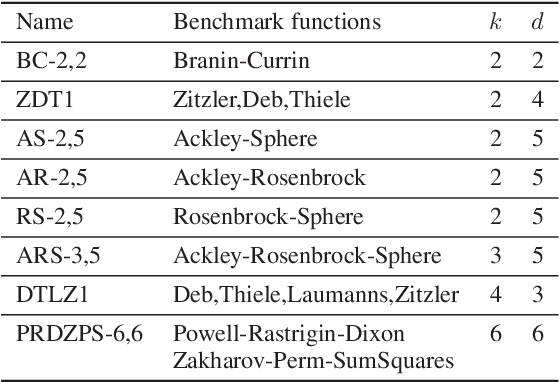
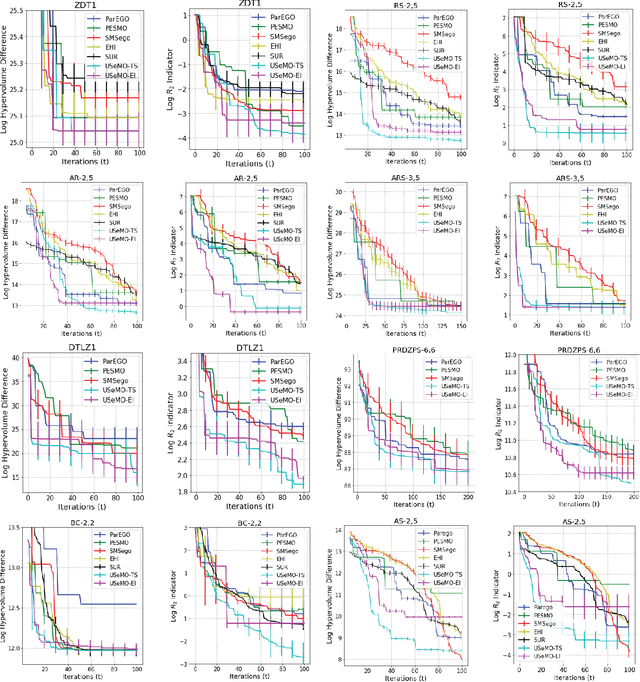
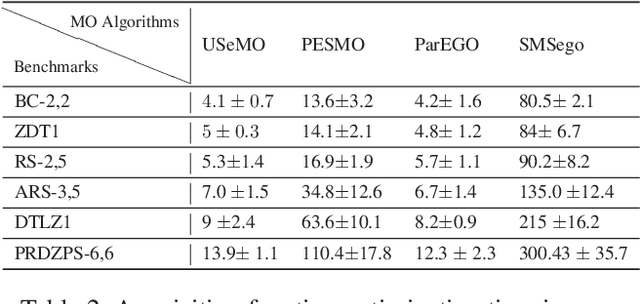
We consider the problem of multi-objective (MO) blackbox optimization using expensive function evaluations, where the goal is to approximate the true Pareto set of solutions while minimizing the number of function evaluations. For example, in hardware design optimization, we need to find the designs that trade-off performance, energy, and area overhead using expensive simulations. We propose a novel uncertainty-aware search framework referred to as USeMO to efficiently select the sequence of inputs for evaluation to solve this problem. The selection method of USeMO consists of solving a cheap MO optimization problem via surrogate models of the true functions to identify the most promising candidates and picking the best candidate based on a measure of uncertainty. We also provide theoretical analysis to characterize the efficacy of our approach. Our experiments on several synthetic and six diverse real-world benchmark problems show that USeMO consistently outperforms the state-of-the-art algorithms.

Bayesian Optimization over Permutation Spaces

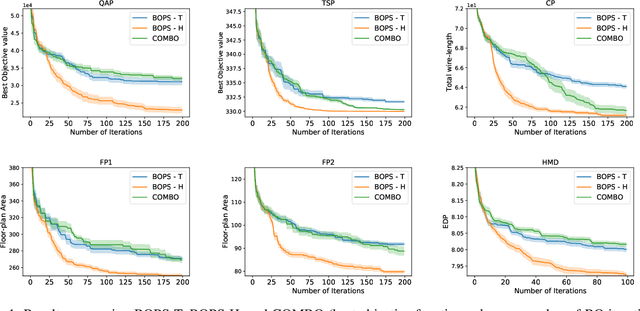
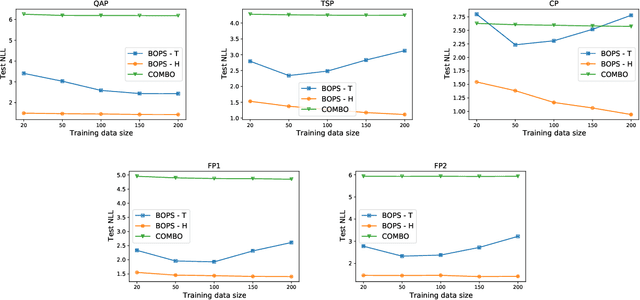
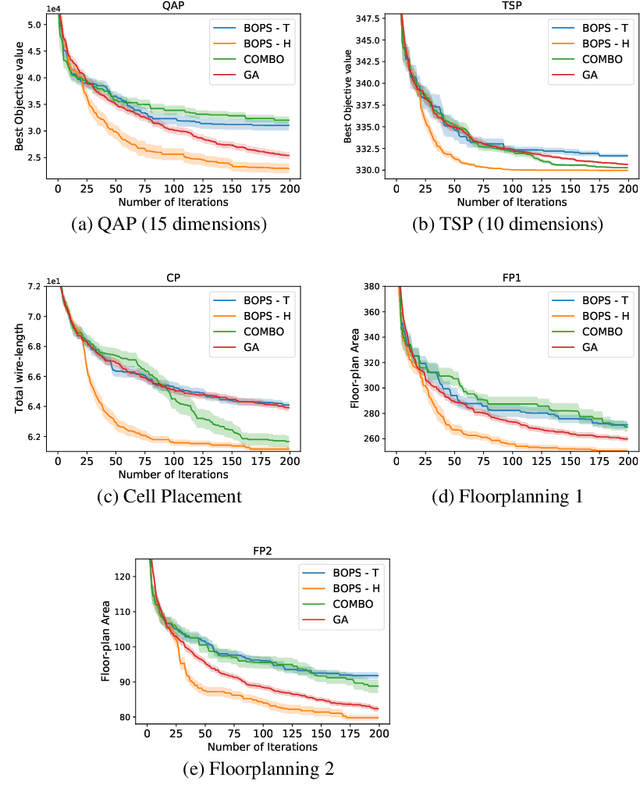
Optimizing expensive to evaluate black-box functions over an input space consisting of all permutations of d objects is an important problem with many real-world applications. For example, placement of functional blocks in hardware design to optimize performance via simulations. The overall goal is to minimize the number of function evaluations to find high-performing permutations. The key challenge in solving this problem using the Bayesian optimization (BO) framework is to trade-off the complexity of statistical model and tractability of acquisition function optimization. In this paper, we propose and evaluate two algorithms for BO over Permutation Spaces (BOPS). First, BOPS-T employs Gaussian process (GP) surrogate model with Kendall kernels and a Tractable acquisition function optimization approach based on Thompson sampling to select the sequence of permutations for evaluation. Second, BOPS-H employs GP surrogate model with Mallow kernels and a Heuristic search approach to optimize expected improvement acquisition function. We theoretically analyze the performance of BOPS-T to show that their regret grows sub-linearly. Our experiments on multiple synthetic and real-world benchmarks show that both BOPS-T and BOPS-H perform better than the state-of-the-art BO algorithm for combinatorial spaces. To drive future research on this important problem, we make new resources and real-world benchmarks available to the community.

Output Space Entropy Search Framework for Multi-Objective Bayesian Optimization

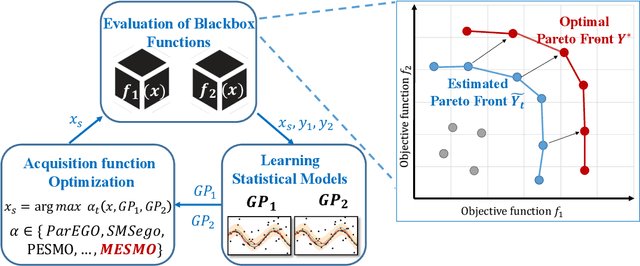
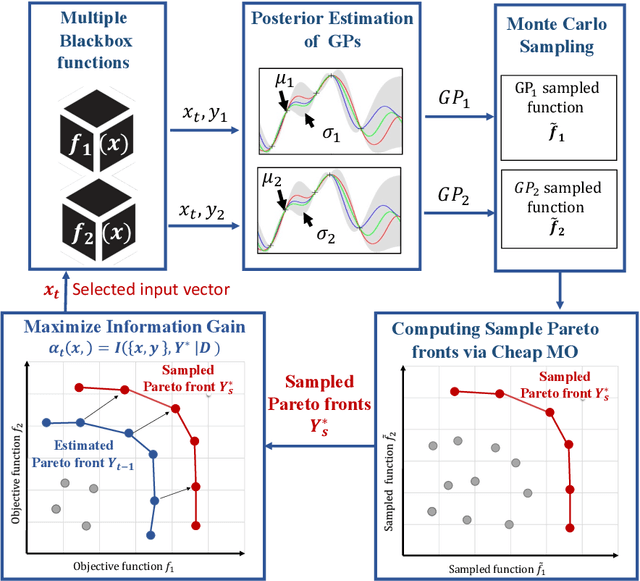
We consider the problem of black-box multi-objective optimization (MOO) using expensive function evaluations (also referred to as experiments), where the goal is to approximate the true Pareto set of solutions by minimizing the total resource cost of experiments. For example, in hardware design optimization, we need to find the designs that trade-off performance, energy, and area overhead using expensive computational simulations. The key challenge is to select the sequence of experiments to uncover high-quality solutions using minimal resources. In this paper, we propose a general framework for solving MOO problems based on the principle of output space entropy (OSE) search: select the experiment that maximizes the information gained per unit resource cost about the true Pareto front. We appropriately instantiate the principle of OSE search to derive efficient algorithms for the following four MOO problem settings: 1) The most basic em single-fidelity setting, where experiments are expensive and accurate; 2) Handling em black-box constraints} which cannot be evaluated without performing experiments; 3) The discrete multi-fidelity setting, where experiments can vary in the amount of resources consumed and their evaluation accuracy; and 4) The em continuous-fidelity setting, where continuous function approximations result in a huge space of experiments. Experiments on diverse synthetic and real-world benchmarks show that our OSE search based algorithms improve over state-of-the-art methods in terms of both computational-efficiency and accuracy of MOO solutions.

Combining Latent Space and Structured Kernels for Bayesian Optimization over Combinatorial Spaces

We consider the problem of optimizing combinatorial spaces (e.g., sequences, trees, and graphs) using expensive black-box function evaluations. For example, optimizing molecules for drug design using physical lab experiments. Bayesian optimization (BO) is an efficient framework for solving such problems by intelligently selecting the inputs with high utility guided by a learned surrogate model. A recent BO approach for combinatorial spaces is through a reduction to BO over continuous spaces by learning a latent representation of structures using deep generative models (DGMs). The selected input from the continuous space is decoded into a discrete structure for performing function evaluation. However, the surrogate model over the latent space only uses the information learned by the DGM, which may not have the desired inductive bias to approximate the target black-box function. To overcome this drawback, this paper proposes a principled approach referred as LADDER. The key idea is to define a novel structure-coupled kernel that explicitly integrates the structural information from decoded structures with the learned latent space representation for better surrogate modeling. Our experiments on real-world benchmarks show that LADDER significantly improves over the BO over latent space method, and performs better or similar to state-of-the-art methods.

Bayesian Optimization over Hybrid Spaces

We consider the problem of optimizing hybrid structures (mixture of discrete and continuous input variables) via expensive black-box function evaluations. This problem arises in many real-world applications. For example, in materials design optimization via lab experiments, discrete and continuous variables correspond to the presence/absence of primitive elements and their relative concentrations respectively. The key challenge is to accurately model the complex interactions between discrete and continuous variables. In this paper, we propose a novel approach referred as Hybrid Bayesian Optimization (HyBO) by utilizing diffusion kernels, which are naturally defined over continuous and discrete variables. We develop a principled approach for constructing diffusion kernels over hybrid spaces by utilizing the additive kernel formulation, which allows additive interactions of all orders in a tractable manner. We theoretically analyze the modeling strength of additive hybrid kernels and prove that it has the universal approximation property. Our experiments on synthetic and six diverse real-world benchmarks show that HyBO significantly outperforms the state-of-the-art methods.

Mercer Features for Efficient Combinatorial Bayesian Optimization

Bayesian optimization (BO) is an efficient framework for solving black-box optimization problems with expensive function evaluations. This paper addresses the BO problem setting for combinatorial spaces (e.g., sequences and graphs) that occurs naturally in science and engineering applications. A prototypical example is molecular optimization guided by expensive experiments. The key challenge is to balance the complexity of statistical models and tractability of search to select combinatorial structures for evaluation. In this paper, we propose an efficient approach referred as Mercer Features for Combinatorial Bayesian Optimization (MerCBO). The key idea behind MerCBO is to provide explicit feature maps for diffusion kernels over discrete objects by exploiting the structure of their combinatorial graph representation. These Mercer features combined with Thompson sampling as the acquisition function allows us to employ tractable solvers to find next structures for evaluation. Experiments on diverse real-world benchmarks demonstrate that MerCBO performs similarly or better than prior methods. The source code is available at https://github.com/aryandeshwal/MerCBO .