Sample-Efficient Bayesian Optimization with Transfer Learning for Heterogeneous Search Spaces

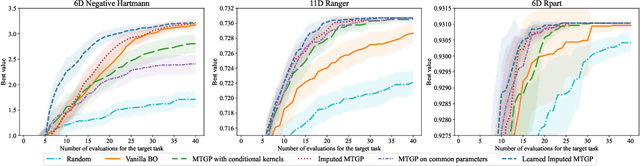
Bayesian optimization (BO) is a powerful approach to sample-efficient optimization of black-box functions. However, in settings with very few function evaluations, a successful application of BO may require transferring information from historical experiments. These related experiments may not have exactly the same tunable parameters (search spaces), motivating the need for BO with transfer learning for heterogeneous search spaces. In this paper, we propose two methods for this setting. The first approach leverages a Gaussian process (GP) model with a conditional kernel to transfer information between different search spaces. Our second approach treats the missing parameters as hyperparameters of the GP model that can be inferred jointly with the other GP hyperparameters or set to fixed values. We show that these two methods perform well on several benchmark problems.

Robust Multi-Objective Bayesian Optimization Under Input Noise

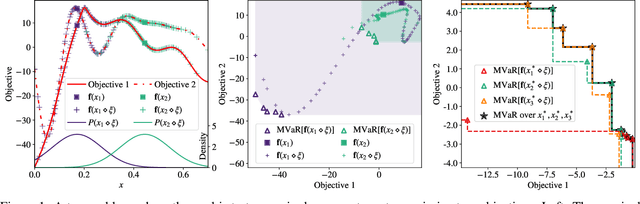
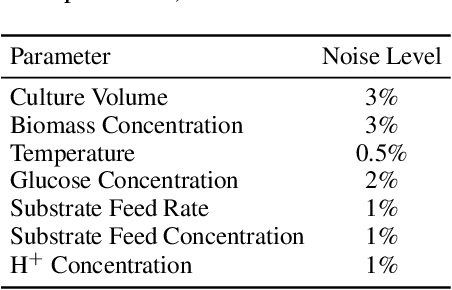
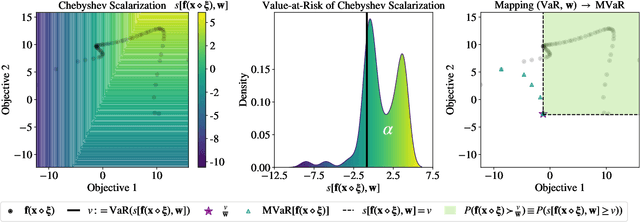
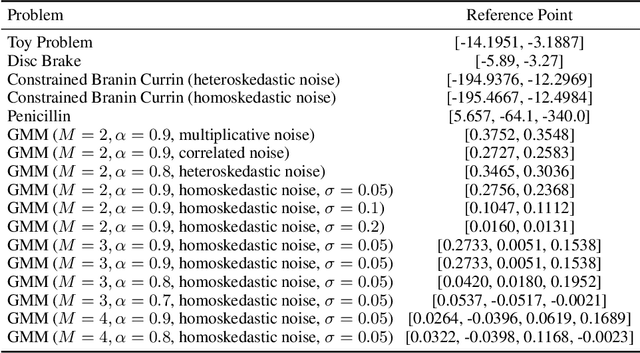
Bayesian optimization (BO) is a sample-efficient approach for tuning design parameters to optimize expensive-to-evaluate, black-box performance metrics. In many manufacturing processes, the design parameters are subject to random input noise, resulting in a product that is often less performant than expected. Although BO methods have been proposed for optimizing a single objective under input noise, no existing method addresses the practical scenario where there are multiple objectives that are sensitive to input perturbations. In this work, we propose the first multi-objective BO method that is robust to input noise. We formalize our goal as optimizing the multivariate value-at-risk (MVaR), a risk measure of the uncertain objectives. Since directly optimizing MVaR is computationally infeasible in many settings, we propose a scalable, theoretically-grounded approach for optimizing MVaR using random scalarizations. Empirically, we find that our approach significantly outperforms alternative methods and efficiently identifies optimal robust designs that will satisfy specifications across multiple metrics with high probability.

Bayesian Optimization of Risk Measures

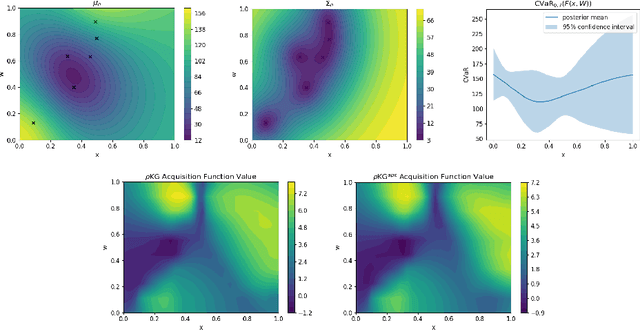
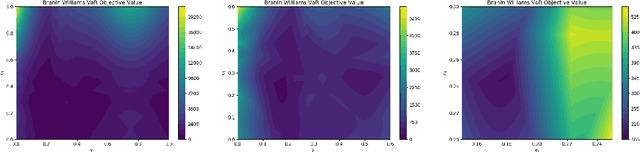
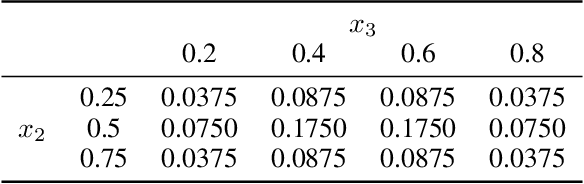
We consider Bayesian optimization of objective functions of the form $\rho[ F(x, W) ]$, where $F$ is a black-box expensive-to-evaluate function and $\rho$ denotes either the VaR or CVaR risk measure, computed with respect to the randomness induced by the environmental random variable $W$. Such problems arise in decision making under uncertainty, such as in portfolio optimization and robust systems design. We propose a family of novel Bayesian optimization algorithms that exploit the structure of the objective function to substantially improve sampling efficiency. Instead of modeling the objective function directly as is typical in Bayesian optimization, these algorithms model $F$ as a Gaussian process, and use the implied posterior on the objective function to decide which points to evaluate. We demonstrate the effectiveness of our approach in a variety of numerical experiments.