Cost-aware Bayesian optimization via the Pandora's Box Gittins index

Bayesian optimization is a technique for efficiently optimizing unknown functions in a black-box manner. To handle practical settings where gathering data requires use of finite resources, it is desirable to explicitly incorporate function evaluation costs into Bayesian optimization policies. To understand how to do so, we develop a previously-unexplored connection between cost-aware Bayesian optimization and the Pandora's Box problem, a decision problem from economics. The Pandora's Box problem admits a Bayesian-optimal solution based on an expression called the Gittins index, which can be reinterpreted as an acquisition function. We study the use of this acquisition function for cost-aware Bayesian optimization, and demonstrate empirically that it performs well, particularly in medium-high dimensions. We further show that this performance carries over to classical Bayesian optimization without explicit evaluation costs. Our work constitutes a first step towards integrating techniques from Gittins index theory into Bayesian optimization.

Multi-Armed Bandits with Interference

Experimentation with interference poses a significant challenge in contemporary online platforms. Prior research on experimentation with interference has concentrated on the final output of a policy. The cumulative performance, while equally crucial, is less well understood. To address this gap, we introduce the problem of {\em Multi-armed Bandits with Interference} (MABI), where the learner assigns an arm to each of $N$ experimental units over a time horizon of $T$ rounds. The reward of each unit in each round depends on the treatments of {\em all} units, where the influence of a unit decays in the spatial distance between units. Furthermore, we employ a general setup wherein the reward functions are chosen by an adversary and may vary arbitrarily across rounds and units. We first show that switchback policies achieve an optimal {\em expected} regret $\tilde O(\sqrt T)$ against the best fixed-arm policy. Nonetheless, the regret (as a random variable) for any switchback policy suffers a high variance, as it does not account for $N$. We propose a cluster randomization policy whose regret (i) is optimal in {\em expectation} and (ii) admits a high probability bound that vanishes in $N$.

Bayesian Optimization of Risk Measures

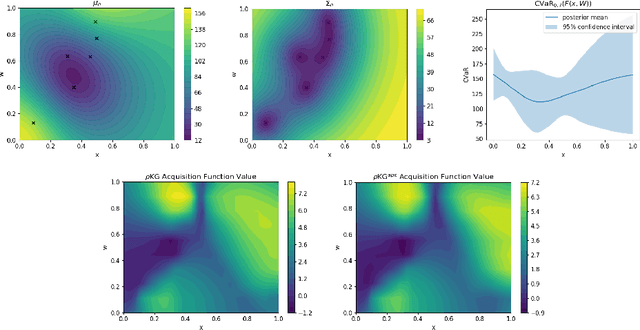
We consider Bayesian optimization of objective functions of the form $\rho[ F(x, W) ]$, where $F$ is a black-box expensive-to-evaluate function and $\rho$ denotes either the VaR or CVaR risk measure, computed with respect to the randomness induced by the environmental random variable $W$. Such problems arise in decision making under uncertainty, such as in portfolio optimization and robust systems design. We propose a family of novel Bayesian optimization algorithms that exploit the structure of the objective function to substantially improve sampling efficiency. Instead of modeling the objective function directly as is typical in Bayesian optimization, these algorithms model $F$ as a Gaussian process, and use the implied posterior on the objective function to decide which points to evaluate. We demonstrate the effectiveness of our approach in a variety of numerical experiments.

Unbiased Comparative Evaluation of Ranking Functions

Eliciting relevance judgments for ranking evaluation is labor-intensive and costly, motivating careful selection of which documents to judge. Unlike traditional approaches that make this selection deterministically, probabilistic sampling has shown intriguing promise since it enables the design of estimators that are provably unbiased even when reusing data with missing judgments. In this paper, we first unify and extend these sampling approaches by viewing the evaluation problem as a Monte Carlo estimation task that applies to a large number of common IR metrics. Drawing on the theoretical clarity that this view offers, we tackle three practical evaluation scenarios: comparing two systems, comparing $k$ systems against a baseline, and ranking $k$ systems. For each scenario, we derive an estimator and a variance-optimizing sampling distribution while retaining the strengths of sampling-based evaluation, including unbiasedness, reusability despite missing data, and ease of use in practice. In addition to the theoretical contribution, we empirically evaluate our methods against previously used sampling heuristics and find that they generally cut the number of required relevance judgments at least in half.

A Hierarchical Distance-dependent Bayesian Model for Event Coreference Resolution

We present a novel hierarchical distance-dependent Bayesian model for event coreference resolution. While existing generative models for event coreference resolution are completely unsupervised, our model allows for the incorporation of pairwise distances between event mentions -- information that is widely used in supervised coreference models to guide the generative clustering processing for better event clustering both within and across documents. We model the distances between event mentions using a feature-rich learnable distance function and encode them as Bayesian priors for nonparametric clustering. Experiments on the ECB+ corpus show that our model outperforms state-of-the-art methods for both within- and cross-document event coreference resolution.